
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Фурье преобразование | Фурье преобразование (далее Ф) (данной функции), функция, выражающаяся через данную функцию f (x) формулой:
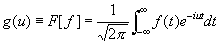 , (1) , (1)
Если функция f (x) четная, то ее ф. п. равно
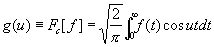 (2) (2)
(косинус-преобразование), а если f (x) — нечетная функция, то
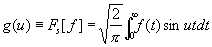 (3) (3)
(синус-преобразование). Формулы (1), (2) и (3) обратимы, т. е. для четных функций
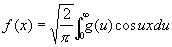 , (4) , (4)
а для нечетных функций
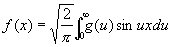 . (5) . (5)
В общем случае имеет место формула
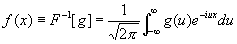 . (6) . (6)
Каждой операции над функциями соответствует операция над их Ф, которая во многих случаях проще соответствующей операции над f (x). Например, Ф f"(x) является iug (u). Если
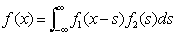 , (7) , (7)
то g (u) = g1(u) g2(u). Для f (x + а) Ф является eiuag (u), а для c1f1(x) + c2f2 (x) — функция c1g1(u) + c2g2(u).
Если существует 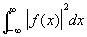 , то интегралы в формулах (1) и (6) сходятся в среднем (см. Сходимость), причем , то интегралы в формулах (1) и (6) сходятся в среднем (см. Сходимость), причем
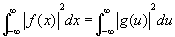 (8) (8)
(теорема Планшереля). Формула (8) является обобщением на Ф формулы Парсеваля (см. Парсеваля равенство) для рядов Фурье (см. Фурье ряд). Физический смысл формулы (8) заключается в равенстве энергии некоторого колебания сумме энергий его гармонических компонент. Отображение : f (x) ® g (u) является унитарным оператором в гильбертовом пространстве функций f (x), — ¥ < x < ¥, с интегрируемым квадратом. Этот оператор может быть представлен также в виде
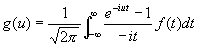 . (9) . (9)
При некоторых условиях на f (x) справедлива формула Пуассона
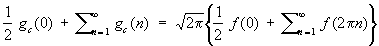 , ,
находящая применение в теории тэта-функций.
Если функция f (x) достаточно быстро убывает, то ее Ф можно определить и при некоторых комплексных значениях u = v + iw. Например, если существует 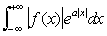 , а > 0, то Ф определено при |w| < а. Ф при комплексных значениях тесно связано с двусторонним преобразованием Лапласа (см. Лапласа преобразование) , а > 0, то Ф определено при |w| < а. Ф при комплексных значениях тесно связано с двусторонним преобразованием Лапласа (см. Лапласа преобразование)
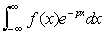 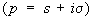 . .
Оператор Ф может быть расширен на более обширные классы функций, нежели совокупность суммируемых функций (например, для функций f (x) таких, что (1 + |x|)–1f (x) суммируема, Ф определяется формулой (9)), и даже на некоторые классы обобщенных функций (т. н. медленного роста).
Имеются обобщения Ф Одно из них использует различного рода специальные функции, например Бесселя функции, это направление получает завершение в теории представлений непрерывных групп. Другим является т. н. преобразование Фурье — Стилтьеса, широко применяемое, например, в теории вероятностей; оно определяется для произвольной ограниченной неубывающей функции j(x) Стилтьеса интегралом
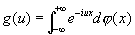 (10) (10)
и называется характеристической функцией распределения j. Для представимости функции g (u) в виде (10) необходимо и достаточно, чтобы при любых u1,..., un, x1,...,xn было
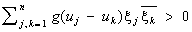
(теорема Бохнера — Хинчина).
Ф, первоначально возникшее в теории теплопроводности, имеет многочисленные применения как в самой математике (например, при решении дифференциальных, разностных и интегральных уравнений, в теории специальных функций и т.д.), так и в различных разделах теоретической физики. Например, Ф стало стандартным аппаратом квантовой теории поля, широко используется в методе функций Грина для неравновесных задач квантовой механики и термодинамики, в теории рассеяния и т.д.
Лит.: Снеддон И., Преобразование Фурье, пер. с англ., М., 1955; Владимиров В. С., Обобщенные функции в математической физике, М., 1976.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.02.2026 13:09:17
|

|

|
 |
|

|
 |
 |
 |
|