
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Фурье коэффициенты | Фурье коэффициенты (далее Ф) коэффициенты
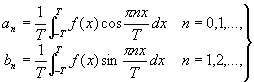 (*) (*)
разложения функции f (x), имеющей период 2T, в ряд Фурье (см. Фурье ряд). Формулы (*) называют формулами Эйлера — Фурье. Непрерывная функция f (x) однозначно определяется своими коэффициентами Фурье. Ф интегрируемой функции f (x) стремятся к нулю при n ® ¥, причем скорость их убывания зависит от дифференциальных свойств функции f (x). Например, если f (x) имеет k непрерывных производных, то существует такое число с, что |an| £ c/nk, |bn| £ c/nk. Ф связаны с f (x) также следующим неравенством:
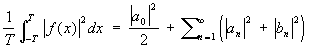
(см. Парсеваля равенство). Ф функции f (x) по любой нормированной ортогональной на отрезке (а, b) системе функций j1(x), j2(x),..., jn (x),... (см. Ортогональная система функций) равны
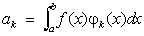 . .
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.02.2026 13:14:08
|

|

|
 |
|

|
 |
 |
 |
|