
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Функциональный определитель | Функциональный определитель (далее Ф) определитель, элементами которого являются функции одного или многих переменных. Наиболее важные примеры Ф — вронскиан, играющий важную роль в теории линейных дифференциальных уравнений высшего порядка, гессиан, применяемый в теории алгебраических кривых, и якобиан, используемый при преобразовании кратных интегралов, установлении независимости системы функций и др. вопросах теории функций многих переменных. Производная Ф D (x) = |aik (x)| n-го порядка равна сумме n Ф, матрицы которых получаются из матрицы ||aik (x)|| соответственно дифференцированием элементов первого, второго,..., n-го столбца. Например, если
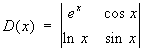 , ,
то
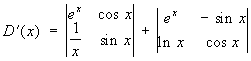 . .
Иногда термин "Ф" применяется для обозначения якобиана.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:09:50
|

|

|
 |
|

|
 |
 |
 |
|