
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Флуктуации | Флуктуации (далее Ф) (от лат. fluctuatio – колебание), случайные отклонения наблюдаемых физических величин от их средних значений. Ф происходят у любых величин, зависящих от случайных факторов и описываемых методами статистики (см. Случайный процесс). Количественная характеристика Ф основана на методах математической статистики и вероятностей теории. Простейшей мерой Ф величины х служит ее дисперсия s2x, т. е. средний квадрат отклонения х от ее среднего значения 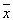 , s2x = , s2x = 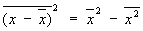 , где черта сверху означает статистическое усреднение. Эквивалентной мерой Ф является квадратичное отклонение Ox, равное корню квадратному из дисперсии, или его относительная величина dx = sх/х. , где черта сверху означает статистическое усреднение. Эквивалентной мерой Ф является квадратичное отклонение Ox, равное корню квадратному из дисперсии, или его относительная величина dx = sх/х.
В статистической физике наблюдаемые значения физических величин очень близки к их средним статистическим значениям, т. е. Ф, вызванные случайным тепловым движением частиц (например, Ф средней энергии, плотности, давления), очень малы. Однако они имеют принципиальное значение, ограничивая пределы применимости термодинамических понятий лишь большими (содержащими очень много частиц) системами, для которых Ф значительно меньше самих флуктуирующих величин. Существование Ф уточняет смысл второго начала термодинамики: утверждение о невозможности вечного двигателя 2-го рода остается справедливым, но оказываются возможными Ф системы из равновесного состояния в неравновесные, обладающие меньшей энтропией; однако на основе таких Ф нельзя построить вечный двигатель 2-го рода. Для средних величин остается справедливым закон возрастания энтропии в изолированной системе.
Основы теории Ф были заложены в работах Дж. Гиббса, А. Эйнштейна, М. Смолуховского.
С помощью Гиббса распределений можно вычислить Ф в состоянии статистического равновесия для систем, находящихся в различных физических условиях; при этом Ф выражаются через равновесные термодинамические параметры и производные потенциалов термодинамических. Например, для систем с постоянным объемом и постоянным числом частиц , находящихся в контакте с термостатом (с температурой Т), каноническое распределение Гиббса дает для Ф энергии (Е): 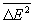 = (kT)2, где k – Больцмана постоянная, – теплоемкость при постоянном объеме. Такое же выражение для Ф справедливо и в случае квантовой статистики, различаются лишь явные выражения для . Для систем с постоянным объемом в контакте с термостатом и резервуаром частиц большое каноническое распределение Гиббса дает для Ф числа частиц: = (kT)2, где k – Больцмана постоянная, – теплоемкость при постоянном объеме. Такое же выражение для Ф справедливо и в случае квантовой статистики, различаются лишь явные выражения для . Для систем с постоянным объемом в контакте с термостатом и резервуаром частиц большое каноническое распределение Гиббса дает для Ф числа частиц: 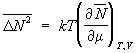 , где m – химический потенциал. В приведенных примерах флуктуируют пропорциональные объему (т. н. экстенсивные) величины. Их относительные квадратичные Ф , где m – химический потенциал. В приведенных примерах флуктуируют пропорциональные объему (т. н. экстенсивные) величины. Их относительные квадратичные Ф 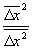 пропорциональны величине 1/ (нормальные Ф) и, следовательно, очень малы. В точках фазовых переходов Ф сильно возрастают, и их относительное убывание с может быть более медленным. пропорциональны величине 1/ (нормальные Ф) и, следовательно, очень малы. В точках фазовых переходов Ф сильно возрастают, и их относительное убывание с может быть более медленным.
Для более детальной характеристики Ф нужно знать функцию распределения их вероятностей. Вероятность w (x1,..., хп) Ф некоторых величин x1,..., хп из состояния неполного термодинамического равновесия с энтропией (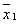 ,..., ,..., 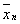 ) в состояние с энтропией (x1,..., хп) определяется формулой Больцмана: ) в состояние с энтропией (x1,..., хп) определяется формулой Больцмана:
w (x1,..., хп)/w (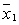 ,..., ,..., 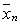 ) = exp { (x1,..., хп) – ( ) = exp { (x1,..., хп) – (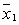 ,..., ,..., 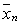 )} )}
(поскольку энтропия равна логарифму статистического веса, или термодинамической вероятности состояния). Под энтропией состояния неполного равновесия понимают энтропию вспомогательного равновесного состояния, которое характеризуется такими же средними значениями xi, как и данное неравновесное. Для малых Dxi = xi – xi эта формула переходит в распределение Гаусса:
w (x1,..., хп) = А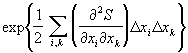 , ,
где А – константа, определяемая из условия нормировки вероятности к 1.
Можно найти не только Ф величин xi, но и корреляции между ними 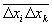 , определяющие их взаимное влияние (лишь в случае статистически независимых величин , определяющие их взаимное влияние (лишь в случае статистически независимых величин 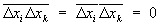 ); примером могут служить корреляции температуры и давления: ); примером могут служить корреляции температуры и давления: 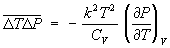 (температура связана со средней энергией), объема и давления: (температура связана со средней энергией), объема и давления: 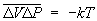 . Для физических величин А (х, t), В (х, t), зависящих от координат (x) и времени (t), вообще говоря, имеют место пространственно-временные корреляции между их Ф в различных точках пространства в различные моменты времени: . Для физических величин А (х, t), В (х, t), зависящих от координат (x) и времени (t), вообще говоря, имеют место пространственно-временные корреляции между их Ф в различных точках пространства в различные моменты времени:
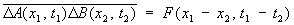 ; ;
функции называются пространственно-временными корреляционными (или коррелятивными) функциями и в состоянии статистического равновесия зависят лишь от разностей координат и времени. Функции для плотности (n) числа частиц 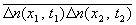 могут быть экспериментально измерены по рассеянию медленных нейтронов или рентгеновских лучей: дважды дифференциальное сечение рассеяния нейтронов определяет фурье-образ пространственно-временной корреляционной функции плотностей частиц в среде. могут быть экспериментально измерены по рассеянию медленных нейтронов или рентгеновских лучей: дважды дифференциальное сечение рассеяния нейтронов определяет фурье-образ пространственно-временной корреляционной функции плотностей частиц в среде.
Ф связаны с неравновесными процессами. Такие неравновесные характеристики системы, как кинетические коэффициенты (см. Кинетика физическая), пропорциональны интегралам по времени от временных корреляционных функций потоков физических величин (формулы Грина – Кубо). Например, электропроводность пропорциональна интегралу от корреляционных функций плотностей токов, коэффициенты теплопроводности, вязкости, диффузии пропорциональны соответственно интегралам от корреляционных функций плотностей потоков тепла, импульса и диффузионного потока.
В общем случае существует связь между Ф физических величин и диссипативными свойствами системы при внешнем возмущении. Реакция системы на некоторое возмущение (т. е. соответствующее изменение некоторой физической величины) определяется т. н. обобщенной восприимчивостью, мнимая часть которой пропорциональна фурье-компоненте временной корреляционной функции возмущений, связанных с данным воздействием (флуктуационно-диссипативная теорема).
Ф в системах заряженных частиц проявляются как хаотические изменения потенциалов, токов или зарядов; они обусловлены как дискретностью электрического заряда, так и тепловым движением носителей заряда. Эти Ф являются причиной электрических шумов и определяют предел чувствительности приборов для регистрации слабых электрических сигналов (см. Ф электрические).
Ф можно наблюдать по рассеянию света: случайные изменения плотности среды из-за Ф вызывают случайные изменения по объему показателя преломления, и в однородной по составу среде или даже в чистом веществе может происходить рассеяние света, как в мутной среде. Это явление особенно заметно в бинарных растворах при температуре, близкой к критической температуре расслаивания, – т. н. критическое рассеяние света. Ф также очень велики в критической точке равновесия жидкость – пар (см. Критические явления). Ф давления проявляются в броуновском движении взвешенных в жидкости (или газе) малых частиц под влиянием нескомпенсированных точно ударов молекул окружающей среды.
Лит.: Эйнштейн А., Смолуховский М., Брауновское движение. Сб., пер. с нем., М. – Л., 1936; Леонтович М. А., Статистическая физика, М. – Л., 1944; Мюнстер А., Теория флуктуаций, в сборнике: Термодинамика необратимых процессов, пер. с англ., М., 1962; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Левин М. Л., Рытов С. М., Теория равновесных тепловых флуктуаций в электродинамике, М., 1967. См. также лит. при ст. Статистическая физика.
Д. Н. Зубарев. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:53:33
|

|

|
 |
|

|
 |
 |
 |
|