
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Уравнения математической физики | Уравнения математической физики (далее У) дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории У характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг У с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование (см. Математическая физика).
Классификация уравнений математической физики. Значительная часть У составляют линейные уравнения с частными производными 2-го порядка общего вида:
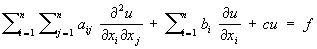 , (1) , (1)
где все коэффициенты aij (aij = aij), bi, с и правая часть f представляют собой заданные функции независимых переменных x1, x2,..., хп (n ³ 2), а u – искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно l) уравнения
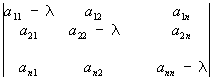 = 0, (2) = 0, (2)
и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все n корней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных n – 1 корней, – к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты aij постоянны, то уравнение (1) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от x1,..., хп, то и корни уравнения (2) зависят от x1,..., хп, а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими).
Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.
Основные примеры уравнений математической физики.
Волновое уравнение:
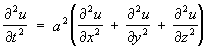
– простейшее уравнение гиперболического типа, а также соответствующие неоднородные уравнения (в правой части которых добавлены известные функции) – телеграфное уравнение и т.д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболического типа во многом аналогичны свойствам приведенных простейших таких уравнений.
Лапласа уравнение:
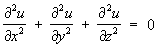
– простейшее уравнение эллиптического типа и соответствующее неоднородное уравнение – Пуассона уравнение. Уравнения и системы эллиптического типа появляются обычно при анализе стационарных состояний. Теплопроводности уравнение:
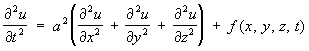
– простейший пример уравнения параболического типа. Уравнения и системы параболического типа появляются обычно при анализе процессов выравнивания.
Первым примером уравнений смешанного типа явилось т. н. уравнение Трикоми:
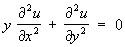
Для этого уравнения полуплоскость 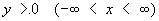 служит зоной эллиптичности, полуплоскость у < 0 – зоной гиперболичности, а прямая у = 0 – зоной параболичности. служит зоной эллиптичности, полуплоскость у < 0 – зоной гиперболичности, а прямая у = 0 – зоной параболичности.
Ряд задач математической физики приводит к интегральным уравнениям различных типов. Так, например, интегральные уравнения Вольтерра возникают в тех задачах физики, в которых существует предпочтительное направление изменения независимого переменного (например, времени, энергии и т.д.). В задаче о крутильных колебаниях возникает некоторое интегро-дифференциальное уравнение.
Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У много усилий было затрачено на отыскание их общего решения. Уже Ж. Д"Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л. Эйлером (1770), П. Лаплас предложил (1773) "каскадный метод", дающий общее решение некоторых др. линейных однородных гиперболических уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значительного класса уравнений, для которых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось что при анализе физических процессов У обычно появляются вместе с дополнительными условиями, характер которых коренным образом влияет на направление исследования решения (см. Краевые задачи, Коши задача).
Широкое распространение получили методы приближенного решения краевых задач, в которых задача сводится к решению системы алгебраических (обычно линейных) уравнений (см. Ритца и Галеркина методы. Сеток метод). При этом за счет увеличения числа неизвестных в системе можно достичь любой степени точности приближения.
Лит.: Владимиров В. С., У, 2 изд., М., 1971; Годунове. К., У, М., 1971; Соболев С. Л., У, 4 изд., М., 1966; Тихонов А. Н., Самарский А. А., У, 4 изд., М., 1972.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 11.03.2026 21:00:29
|

|

|
 |
|

|
 |
 |
 |
|