
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Управляемый случайный процесс | Управляемый случайный процесс (далее У) случайный процесс, вероятностные характеристики которого можно изменять с помощью управляющих воздействий. Основная цель теории У – отыскание оптимальных (или близких к ним) управлений, доставляющих экстремум заданному критерию качества. В простейшем случае управляемых марковских цепей одна из математических постановок задачи нахождения оптимального управления формулируется следующим образом. Пусть Xd = (xn,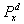 ), n = 0, 1,..., – семейство однородных марковских цепей с конечным числом состояний Е = {0, 1, ..., } и матрицами переходных вероятностей xy (d) = ), n = 0, 1,..., – семейство однородных марковских цепей с конечным числом состояний Е = {0, 1, ..., } и матрицами переходных вероятностей xy (d) = 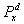 {x1 = у}, зависящих от параметра d, принадлежащего некоторому множеству управляющих воздействий D. Набор функций a = {а0 (x0), a1 (x0, x1),...} со значениями в D называют стратегией, а каждую из функций an = ап (х0,..., хп) – управлением в момент времени n. Каждой стратегии a отвечает управляемая марковская цепь Xa = (хп, {x1 = у}, зависящих от параметра d, принадлежащего некоторому множеству управляющих воздействий D. Набор функций a = {а0 (x0), a1 (x0, x1),...} со значениями в D называют стратегией, а каждую из функций an = ап (х0,..., хп) – управлением в момент времени n. Каждой стратегии a отвечает управляемая марковская цепь Xa = (хп,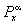 ), n = 0, 1,..., где ), n = 0, 1,..., где
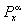 (x0, x1..., хп) = d(х0, х) Рх0х1 (a0 (x0*(... Pxn-1xn (an-1(x0, x1,..., xn-1*( (x0, x1..., хп) = d(х0, х) Рх0х1 (a0 (x0*(... Pxn-1xn (an-1(x0, x1,..., xn-1*(
Пусть: 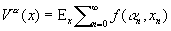
где функция f (d, х) ³ 0 и f (d,0) = 0 (если точка {0} является поглощающим состоянием и f (d, x) = , d Î D, x = 1,..., , то a (x) есть матем. ожидание времени попадания из точки х в точку 0). Функцию
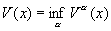
называется ценой, а стратегию а* – оптимальной, если 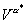 = (x) для всех х Î Е. = (x) для всех х Î Е.
При довольно общих предположениях о множестве D устанавливается, что цена (x) удовлетворяет следующему уравнению оптимальности (уравнению Беллмана):
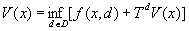 , ,
где
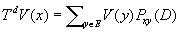 . .
В классе всех стратегий наибольший интерес представляют т. н. однородные марковские стратегии, характеризуемые одной функцией а (х) такой, что an (x0,..., xn) = a (xn) при всех n = 0, 1,...
Следовательно, критерий оптимальности (или достаточное условие оптимальности) может быть использован для проверки того, что данная однородная марковская стратегия является оптимальной: пусть существуют функции a* = а*(х) и * = *(x) такие, что для любого d Î D
0 = f (x, a*(x*( + La£ f (x, d) + Ld*(x)
(Ld = Td – , – единичный оператор), тогда * является ценой (* = ) и стратегия a* = a*(х) является оптимальной.
Лит.: Ховард Р.-А., Динамическое программирование и марковские процессы, пер. с англ., М. 1964.
А. Н. Ширяев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:46:16
|

|

|
 |
|

|
 |
 |
 |
|