
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Унитарное преобразование | Унитарное преобразование (далее У)линейное преобразование
x`i = ui1x1 + ui2x2 +... + uinxn (i = 1, 2,..., n)
с комплексными коэффициентами, сохраняющее неизменной сумму квадратов модулей преобразуемых величин
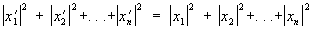
Унитарное преобразование представляет собой аналог (точнее, обобщение) поворота в евклидовой плоскости или вращения в трехмерном евклидовом пространстве на случай n-мерного комплексного векторного пространства, т.к. оно сохраняет для преобразуемого вектора х с компонентами x1, x2,..., xn его длину, равную
 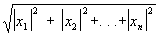 . .
Коэффициенты Унитарное преобразование образуют унитарную матрицу. Совокупность Унитарное преобразование n-мерного комплексного векторного пространства является группой относительно умножения преобразований. В случае, когда коэффициенты uij и преобразуемые величины xi действительны, Унитарное преобразование является ортогональным преобразованием n-мерного действительного векторного пространства.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:11:39
|

|

|
 |
|

|
 |
 |
 |
|