
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Тригонометрия | Тригонометрия (далее Т) (от греч. trígōnon - треугольники ¼метрия), раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Т делится на плоскую, или прямолинейную, и сферическую тригонометрию. Теория тригонометрических функций (гониометрия) и ее приложения к решению плоских прямоугольных и косоугольных треугольников изучаются в средней школе.
Основные формулы плоской Т Пусть а, b, с - стороны треугольника, А, В, С - противолежащие им углы (А+В+С = p), ha, hb, hc - высоты, 2p - периметр, - площадь, 2R - диаметр окружности, описанной около треугольника. Теорема синусов:
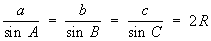 , ,
теорема косинусов:
a2 = b2 + c2 - 2bc cos A,
теорема тангенсов:
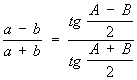 , ,
площадь треугольника:
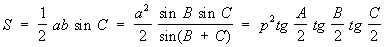 . .
Углы треугольника, если известны стороны, могут быть найдены по теореме косинусов или по формулам вида:
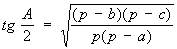 . .
Плоская Т начала развиваться позже сферической, хотя отдельные теоремы ее встречались и раньше. Например, 12-я и 13-я теоремы второй книги "Начал" Евклида (3 в. дон. э.) выражают по существу теорему косинусов. Плоская Т получила развитие у аль-Баттани (2-я половина 9 - начало 10 вв.), Абу-ль-Вефа (10 в.), Бхаскара (12 в.) и Насирэддина Туси (13 в.), которым была уже известна теорема синусов. Теорема тангенсов была получена Региомонтаном (15 в.). Дальнейшие работы в области Т принадлежат Н. Копернику (1-я половина 16 в.), Т Браге (2-я половина 16 в.), Ф. Виету (16 в.), И. Кеплеру (конец 16 - 1-я половина 17 вв.). Современный вид Т получила в работах Л. Эйлера (18 в.).
Лит.: Кочетков Е. С., Кочеткова Е. С., Алгебра и элементарные функции, ч. 1-2, М., 1966. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 07.03.2026 07:04:37
|

|

|
 |
|

|
 |
 |
 |
|