
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Тригонометрические функции | Тригонометрические функции (далее Т), один из важнейших классов элементарных функций.
Для определения Т обычно рассматривают окружность единичного радиуса с двумя взаимно перпендикулярными диаметрами A"A и " (рис. 1). От точки А по окружности откладываются дуги произвольной длины, которые считаются положительными, если откладываются в направлении от А к В (против часовой стрелки), и отрицательными, если они откладываются в направлении от А к " (по часовой стрелке). Если С — конец дуги, имеющей длину j, то проекция радиуса на диаметр A"A называется косинусом дуги j ( = cos j). При этом под проекцией понимается длина направленного отрезка 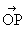 , взятая со знаком плюс, если точка Р лежит на радиусе OA, и со знаком минус, если она лежит на радиусе OA"; Проекция OQ радиуса на диаметр " (равная +OQ, если точка Q лежит на радиусе , и равная -OQ, если она лежит на радиусе ") называется синусом дуги j (OQ = sin j). Т cos j и sin j не могут принимать значений, по абсолютной величине превосходящих 1, то есть , взятая со знаком плюс, если точка Р лежит на радиусе OA, и со знаком минус, если она лежит на радиусе OA"; Проекция OQ радиуса на диаметр " (равная +OQ, если точка Q лежит на радиусе , и равная -OQ, если она лежит на радиусе ") называется синусом дуги j (OQ = sin j). Т cos j и sin j не могут принимать значений, по абсолютной величине превосходящих 1, то есть
|cosj| £ 1, |sinj| £ 1.
Иначе cosj и sinj могут быть определены как прямоугольные декартовы координаты точки С, лежащей на дуге окружности единичного радиуса, центр которой в начале координат, ось абсцисс направлена по диаметру A"A, а ось ординат — по диаметру ".
Так как центральный угол в радианной мере измеряется тем же числом, что и дуга (радиус окружности равен единице), то cosj и sinj можно рассматривать как косинус и синус угла. Вообще под аргументом Т принято понимать число, которое можно рассматривать геометрически как длину дуги или радианную меру угла. Если аргумент Т рассматривают как угол, то его значение может быть выражено и в градусной мере. Для острых углов j (0 < j < p/2), и только для них, Т cos j и sin j можно рассматривать как отношение катетов прямоугольного треугольника, прилежащего углу или противолежащего углу, к гипотенузе. Дуга AB окружности называется 1-й ее четвертью, соответственно дуги BA" — 2-й, A" — 3-й, "A — 4-й четвертями. Для углов j из 1-й четверти: cosj > 0, sinj > 0, из 2-й четверти: cosj < 0, sinj > 0, из 3-й четверти: cosj < 0, sinj < 0, из 4-й четверти: cosj > 0, sinj < 0. Кроме того, cosj — четная функция: cos (—j) = cosj, а sinj — нечетная функция: sin (—j) = —sinj.
С помощью основных Т можно определить другие Т: тангенс tgj = sinj /cosj, котангенс ctgj = cosj /sinj, секанс secj = 1/cosj, косеканс cosecj = 1/sinj. При этом tgj и secj определяются только для таких j, для которых cosj ¹ 0; а ctgj и cosecj для тех j, для которых sinj ¹ 0; функция secj — четная, а функции cosecj, tgj и ctgj — нечетные. Эти функции также могут быть представлены геометрически отрезками прямых (рис. 1): tgj = AL, ctgj = , secj = OL, cosecj = (для острых углов j и соответствующими отрезками для других углов). С этим геометрическим представлением связано и происхождение названий Т Так, латинское tangens означает касательную (tgj изображается отрезком AL касательной к окружности), secans — секущую (secj изображается отрезком OL секущей к окружности). Название "синус" (лат. sinus — изгиб, пазуха) представляет собой перевод арабского "джайб", являющегося, по-видимому, искажением санскритского слова "джива" (буквально — тетива лука), которым математики обозначали синус. Названия "косинус", "котангенс", "косеканс" представляют собой сокращения термина complementi sinus (синус дополнения) и ему подобных, выражающих тот факт, что cosj, ctgj и cosecj равны соответственно синусу, тангенсу и секансу аргумента (дуги или угла), дополнительного к j (до или, в градусной мере, до 90°):
cosj = sin ( — j); ctgj = tg ( — j);
cosecj = sec ( — j).
Подобно синусу и косинусу, остальные Т для острых углов могут рассматриваться как отношения сторон прямоугольного треугольника: тангенс и котангенс как отношения катетов (противолежащего к прилежащему и наоборот), а секанс и косеканс как отношения гипотенузы соответственно к прилежащему и противолежащему катетам.
Так как точка С, являющаяся концом дуги j, служит одновременно концом дуг j + 2p, j + 4p, ¼ (2p — длина окружности), то все Т оказываются периодическими. При этом основным периодом функций sinj, cosj, secj, cosecj является число 2p (угол в 360°), а основным периодом tgj и ctgj — число p (угол в 180°). Графики Т см. на рис. 2.
Значения Т одного и того же аргумента связаны между собой рядом соотношений:
sin2j + cos2j = 1,
tg2j + 1 = sec2j; ctg2j + 1 = cosec2j.
Для некоторых значений аргумента значения Т могут быть получены из геометрических соображений (табл.).
Аргумент< | Т< |
в градусах
|
в радианах
|
sinj
|
cosj
|
tgj
|
ctgj
|
secj
|
cosecj
|
0˚
|
0
|
0
|
1
|
0
|
не существует
|
1
|
не существует
|
30˚
|
p/6
|
1/2
|
Ö3/2 " 0,8660
|
Ö3/3 " 0,5774
|
Ö3 " 1,7322
|
2Ö3/3 " 1,1547
|
2
|
45˚
|
p/4
|
Ö2/2 " 0,7071
|
Ö2/2 " 0,7071
|
1
|
1
|
Ö2 " 1,4142
|
Ö2 " 1,4142
|
60˚
|
p/3
|
Ö3/2 " 0,8660
|
1/2
|
Ö3 "
1,7322
|
Ö3/3 " 0,5774
|
2
|
2Ö3/3 " 1,1547
|
90˚
|
p/2
|
1
|
0
|
не существует
|
0
|
не существует
|
1
|
Для больших значений аргумента можно пользоваться так называемыми формулами приведения, которые позволяют выразить Т любого аргумента через
Т аргумента j, удовлетворяющего соотношению 0 £ j £ или даже 0 £ j £ , что упрощает составление таблиц Т и пользование ими, а также построение графиков. Эти формулы имеют вид:
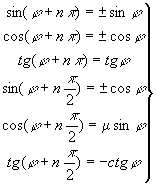 (1) (1)
в первых трех формулах n может быть любым целым числом, причем верхний знак соответствует значению n = 2k, а нижний — значению n = 2k + 1; в последних — n может быть только нечетным числом, причем верхний знак берется при n = 4k + 1, а нижний при n = 4k — 1.
Важнейшими тригонометрическими формулами являются формулы сложения, выражающие Т суммы или разности значений аргумента через Т этих значений:
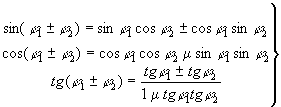 (2) (2)
знаки в левой и правой частях всех формул согласованы, то есть верхнему (нижнему) знаку слева соответствует верхний (нижний) знак справа. Из них, в частности, получаются формулы для Т кратных аргументов, например:
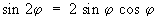
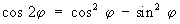
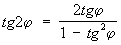
Часто бывают полезны формулы, выражающие степени sin и cos простого аргумента через sin и cos кратного, например:
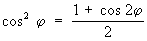 , , 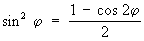 . .
Формулы для cos2j и sin2j можно использовать для нахождения значений Т половинного аргумента:
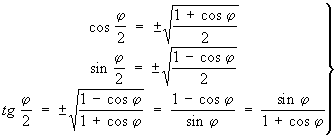 (3) (3)
Знак перед корнем выбирается в зависимости от величины .
Суммы или разности Т различных аргументов могут быть преобразованы в произведения по следующим формулам:
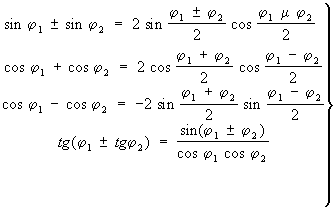 (4) (4)
в первой и последней формулах (4) знаки согласованы. Наоборот, произведения Т могут быть преобразованы в сумму или разность по формулам:
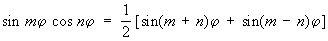 ; ;
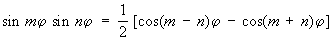 ; ;
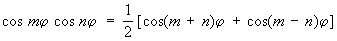 . .
Производные всех Т выражаются через Т:
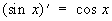 ; ;
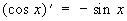 ; ;
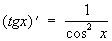 ; ;
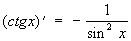 ; ;
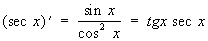 ; ;
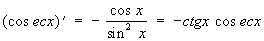 . .
При интегрировании Т получаются Т или их логарифмы:
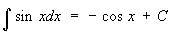 , ,
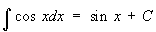 , ,
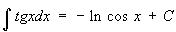 , ,
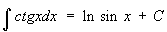 , ,
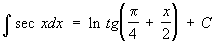 , ,
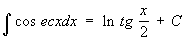 . .
Интегралы от рациональных комбинаций Т всегда являются элементарными функциями.
Все Т допускают разложение в степенные ряды. При этом функции sinx и cosx представляются рядами, сходящимися для всех значений х:
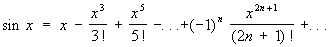 ; ;
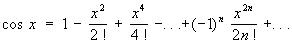 . .
Эти ряды можно использовать для получения приближенных выражений sin x и cos x при малых значениях х:
а) 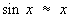 , б) , б) 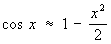 . .
Тригонометрическая система 1, cosx, sinx, cos2x, sin2x, ¼, cosnx, sinnx, ¼, образует на отрезке (—p, p) ортогональную систему функций, что дает возможность представления функций в виде тригонометрических рядов (см. Фурье ряд).
Для комплексных значений аргумента значения Т могут быть определены посредством степенных рядов. Т комплексного аргумента связаны с показательной функцией формулой Эйлера:
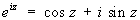 . .
Отсюда можно получить выражения для sin x и cos x через показательные функции чисто мнимого аргумента (которые также называют формулами Эйлера):
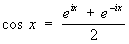 , , 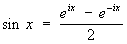
Эти формулы также могут быть использованы для определения значений cosz и sinz для комплексного z. Для чисто мнимых значений z = ix (х — действительное) получаем:
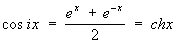 , , 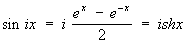 , ,
где ch x и sh x — гиперболические косинус и синус (см. Гиперболические функции). Наоборот,
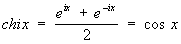 , , 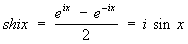 . .
Синус и косинус комплексного аргумента могут принимать действительные значения, превосходящие 1 по абсолютной величине. Например:
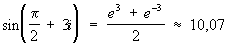 . .
Т комплексного аргумента являются аналитическими функциями, причем sin z и cos z — целые функции, а tg z, ctg z, sec z, cosec z — мероморфные функции. Полюсы tg z и sec z находятся в точках z = p/2 + pn, а ctg z и cosec z в точках z = pn (n = 0, ± 1, ± 2, ¼). Аналитическая функция w = sin z осуществляет конформное отображение полуполосы —p < x < p, y > 0 плоскости z на плоскость w без отрезка действительной оси между точками —1 и +1. При этом семейства лучей х = x0 и отрезков y = y0 переходят соответственно в семейства софокусных гипербол и эллипсов. Вдвое более узкая полоса —p/2 < x < p/2 преобразуется в верхнюю полуплоскость.
Уравнение х = sin y определяет у как многозначную функцию от х. Эта функция является обратной по отношению к синусу и обозначается у = Arc sin x. Аналогично определяются функции, обратные по отношению к косинусу, тангенсу, котангенсу, секансу и косекансу: Arc cos x, Arc tg x, Arc ctg x, Arc sec x, Arc cosec x. Все эти функции называются обратными тригонометрическими функциями (в иностранной литературе иногда эти функции обозначаются sin—1 z, cos—1 z и т.д.).
Т возникли впервые в связи с исследованиями в астрономии и геометрии. Соотношения отрезков в треугольнике и окружности, являющиеся по существу Т, встречаются уже в 3 в. до н. э. в работах математиков Древней Греции — Евклида, Архимеда, Аполлония Пергского и др. Однако эти соотношения не являются у них самостоятельным объектом исследования, так что Т как таковые ими не изучались. Т рассматривались первоначально как отрезки и в такой форме применялись Аристархом (конец 4 — 2-я половина 3 вв. до н. э.), Гиппархом (2 в. до н. э.), Менелаем (1 в. н. э.) и Птолемеем (2 в. н. э.) при решении сферических треугольников. Птолемей составил первую таблицу хорд для острых углов через 30" с точностью до 10—6. Это была первая таблица синусов. Как отношение функция sin j встречается уже у Ариабхаты (конец 5 в.). Функции tg j и ctg j встречаются у аль-Баттани (2-я половина 9 — начало 10 вв.) и Абуль-Вефа (10 в.), который употребляет также sec j и cosec j. Ариабхата знал уже формулу (sin2j + cos2j) = 1, а также формулы (3), с помощью которых построил таблицы синусов для углов через 3°45"; исходя из известных значений Т для простейших аргументов 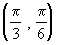 . Бхаскара (12 в.) дал способ построения таблиц через 1 с помощью формул (2). Формулы (4) выводились Региомонтаном (15 в.) и Дж. Непером в связи с изобретением последним логарифмов (1614). Региомонтан дал таблицу значений синуса через 1". Разложение Т в степенные ряды получено И. Ньютоном (1669). В современную форму теорию Т привел Л. Эйлер (18 в.). Ему принадлежат определение Т для действительного и комплексного аргументов, принятая ныне символика, установление связи с показательной функцией, ортогональности системы синусов и косинусов. . Бхаскара (12 в.) дал способ построения таблиц через 1 с помощью формул (2). Формулы (4) выводились Региомонтаном (15 в.) и Дж. Непером в связи с изобретением последним логарифмов (1614). Региомонтан дал таблицу значений синуса через 1". Разложение Т в степенные ряды получено И. Ньютоном (1669). В современную форму теорию Т привел Л. Эйлер (18 в.). Ему принадлежат определение Т для действительного и комплексного аргументов, принятая ныне символика, установление связи с показательной функцией, ортогональности системы синусов и косинусов.
Лит.: Кочетков Е. С., Кочеткова Е. С., Алгебра и элементарные функции, ч. 1—2, М., 1966; Шабат Б. В., Введение в комплексный анализ, М., 1969, с. 61—65.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:01:37
|

|

|
 |
|

|
 |
 |
 |
|