
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Траектория (физич., математич.) | Траектория (далее Т) (от позднелат. trajectorius — относящийся к перемещению), непрерывная линия, которую описывает точка при своем движении. Если Т (физич., математич.) — прямая линия, движение точки называется прямолинейным, в противном случае — криволинейным. Вид Т (физич., математич.) свободной материальной точки зависит от действующих на точку сил, начальных условий движения и от того, по отношению к какой системе отсчета движение рассматривается; для несвободной точки вид Т (физич., математич.) зависит еще от наложенных связей (см. Связи механические).
Например, по отношению к Земле (если пренебречь ее суточным вращением) Т (физич., математич.) свободной материальной точки, отпущенной без начальной скорости и движущейся под действием силы тяжести, будет прямая линия (вертикаль), а если точке сообщить начальную скорость u0, не направленную вдоль вертикали, то при отсутствии сопротивления воздуха ее Т (физич., математич.) будет парабола (рис. 1).
Т (физич., математич.) точки, движущейся в центральном поле тяготения, в зависимости от величины начальной скорости может быть эллипс, парабола или гипербола (в частных случаях — прямая линия или окружность). Так, в поле тяготения Земли, если считать его центральным и пренебречь сопротивлением среды, Т (физич., математич.) точки, получившей вблизи поверхности Земли начальную скорость u0, направленную горизонтально (рис. 2), будет: окружность, когда 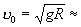 7,9 км/сек (первая космическая скорость); эллипс, когда 7,9 км/сек (первая космическая скорость); эллипс, когда 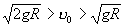 ; парабола, когда ; парабола, когда 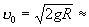 11,2 км/сек (вторая космическая скорость) и гипербола, когда 11,2 км/сек (вторая космическая скорость) и гипербола, когда 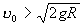 . Здесь R — радиус Земли, g— ускорение силы тяготения вблизи земной поверхности, а движение рассматривается по отношению к осям, перемещающимся вместе с центром Земли поступательно относительно звезд; для тела (например, спутника) все сказанное относится к Т (физич., математич.) его центра тяжести. Если же направление u0 не будет ни горизонтальным, ни вертикальным, то при . Здесь R — радиус Земли, g— ускорение силы тяготения вблизи земной поверхности, а движение рассматривается по отношению к осям, перемещающимся вместе с центром Земли поступательно относительно звезд; для тела (например, спутника) все сказанное относится к Т (физич., математич.) его центра тяжести. Если же направление u0 не будет ни горизонтальным, ни вертикальным, то при 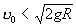 Т (физич., математич.) точки будет представлять собой дугу эллипса, пересекающую поверхность Земли; таковы Т (физич., математич.) центра тяжести баллистических ракет. Т (физич., математич.) точки будет представлять собой дугу эллипса, пересекающую поверхность Земли; таковы Т (физич., математич.) центра тяжести баллистических ракет.
Пример несвободной точки — небольшой груз, подвешенный на нити (см. Маятник). Если нить отклонить от вертикали и отпустить без начальной скорости, то Т (физич., математич.) груза будет дугой окружности, а если при этом грузу сообщить начальную скорость, не лежащую в плоскости отклонения нити, то Т (физич., математич.) груза могут быть кривые довольно сложного вида, лежащие на поверхности сферы (сферический маятник), но в частном случае это может быть окружность, лежащая в горизонтальной плоскости (конический маятник).
Т (физич., математич.) точек твердого тела зависят от закона движения тела. При поступательном движении тела Т (физич., математич.) всех его точек одинаковы, а во всех других случаях движения эти Т (физич., математич.) будут вообще разными для разных точек тела. Например, у колеса автомобиля на прямолинейном участке пути Т (физич., математич.) точки обода колеса по отношению к шоссе будет циклоида, а Т (физич., математич.) центра колеса — прямая линия. По отношению же к кузову автомобиля Т (физич., математич.) точки обода будет окружность, а центр колеса — неподвижен.
Определение Т (физич., математич.) имеет важное значение как при теоретических исследованиях, так и при решении многих практических задач.
С. М. Тарг.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:48:09
|

|

|
 |
|

|
 |
 |
 |
|