
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Тернера метод | Тернера метод (далее Т) один из способов определения положений светил на небесной сфере, применяемый в астрофотографии. Положения звезд, планет, искусственных спутников Земли и др. небесных светил определяются на астронегативах (спутникограммах) относительно так называемых опорных звезд — звезд, для которых экваториальные координаты известны из каталогов. В Т устанавливается математическая зависимость между системой прямоугольных (идеальных) координат опорных звезд, вычисленных по их известным экваториальным координатам, и системой квазипрямоугольных координат, измеренных на астронегативе. Т предложен Г. Х. Тернером в 1893.
В Т зависимость между идеальными x, h и измеренными х, у координатами небесных светил записывается в виде степенных рядов (редукционных уравнений Тернера):
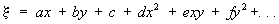
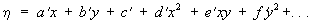
где а, b, с,..., a", b`, c`...— редукционные коэффициенты, называемые постоянными пластинки, которые вычисляются способом наименьших квадратов по системам уравнений Тернера, составленных для опорных звезд раздельно для x и h. Полученные таким образом зависимости используются для преобразования измеренных на астронегативе координат х и у исследуемого светила в идеальные координаты x и h, с помощью которых затем вычисляются его экваториальные координаты. Для современных широкоугольных астрографов применяются усложненные виды редукционных уравнений, например,
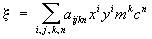 , ,
где aijkn — редукционные постоянные пластинки, m — звездная величина, с — характеристика спектрального класса звезды (аналогичная зависимость и для координаты h). Вид используемого при определении координат небесного светила редукционного уравнения зависит от качества поля астрографа и поставленной задачи. Так, в случае расположения определяемого светила и опорных звезд на небольшой части астронегатива ограничиваются лишь первыми тремя (линейными) членами уравнений.
Лит.: Подобед В. В., Нестеров В. В., Общая астрометрия, М., 1975.
В. В. Подобед. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:52:23
|

|

|
 |
|

|
 |
 |
 |
|