
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Тейлора формула | Тейлора формула (далее Т) формула
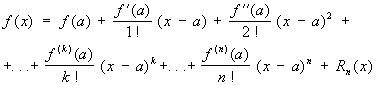
изображающая функцию f (x), имеющую n-ю производную f (n)(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена Rn (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) n (то есть Rn (x) = an (x)(x—a) n, где an (x) ® 0 при х ® а). Если в интервале между а и х существует (n + 1)-я производная, то Rn (x) можно представить в видах:
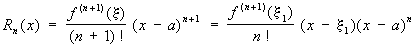 , ,
где x и x1 — какие-то точки указанного интервала (остаточный член Т в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. имеет в точке а соприкосновение не ниже n-го порядка с графиком функции f (x). Т применяют для исследования функций и для приближенных вычислений.
Лит.: Хинчин А. Я., Краткий курс математического анализа, М.. 1953; Фихтенгольц Г. М.. Курс дифференциального и интегрального исчисления, 7 изд., т. 1, М.. 1969. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:22:46
|

|

|
 |
|

|
 |
 |
 |
|