
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Тейлора ряд | Тейлора ряд (далее Т) степенной ряд вида
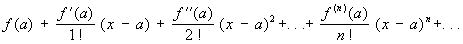 , (1) , (1)
где f (x) — функция, имеющая при х = а производные всех порядков. Во многих практически важных случаях этот ряд сходится к f (x) на некотором интервале с центром в точке а:
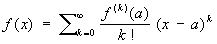 (2) (2)
(эта формула опубликована в 1715 Б. Тейлором). Разность Rn (x) = f (x) — n (x), где n (x) — сумма первых n + 1 членов ряда (1), называется остаточным членом Т Формула (2) справедлива, если 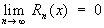 . Т можно представить в виде . Т можно представить в виде
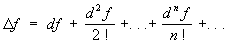 , ,
применимом и к функциям многих переменных.
При а = 0 разложение функции в Т (исторически неправильно называемый в этом случае рядом Маклорена; см. Маклорена ряд) принимает вид:
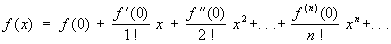 , ,
в частности:
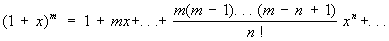 (3) (3)
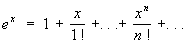 (4) (4)
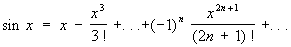 (5) (5)
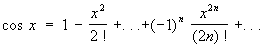 (6) (6)
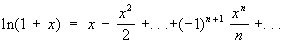 .(7) .(7)
Ряд (3), являющийся обобщением на случай дробных и отрицательных показателей формулы бинома Ньютона, сходится: при -1< х < 1, если m < -1; при -1< x £ 1, если -1< m < 0; при -1 £ x £ 1, если m > 0. Ряды (4), (5) и (6) сходятся при любых значениях х, ряд (7) сходится при -1< x £ 1.
Функция f (z) комплексного переменного z, регулярная в точке а, раскладывается в Т по степеням z — а внутри круга с центром в точке я и с радиусом, равным расстоянию от а до ближайшей особой точки функции f (z). Вне этого круга Т расходится, поведение же его на границе круга сходимости может быть весьма сложным. Радиус круга сходимости выражается через коэффициенты Т (см. Радиус сходимости).
Т является мощным аппаратом для исследования функций и для приближенных вычислений. См. также Тейлора формула.
Лит.: Хинчин А. Я., Краткий курс математического анализа, М., 1953; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:44:04
|

|

|
 |
|

|
 |
 |
 |
|