|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Стокса формула | Стокса формула (далее С) формула преобразования криволинейного интеграла по замкнутому контуру L в поверхностный интеграл по поверхности , ограниченной контуром L. С имеет вид:
 ,
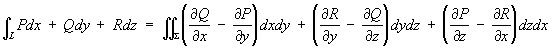причем направление обхода контура L должно быть согласовано с ориентацией поверхности . В векторной форме С приобретает вид:
 ,
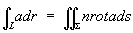где а = Pi + Qj + Rk, dr — элемент контура L, ds — элемент поверхности , n — единичный вектор внешней нормали к этой поверхности. Физический смысл С состоит в том, что циркуляция векторного поля по контуру L равна потоку вихря поля через поверхность . С предложена Дж. Г. Стоксом в 1854.
В гидромеханике формулой Стокса иногда называют Стокса закон.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.12.2024 13:50:55
|
|
|
|
|
|
|
|
|
|
|
