
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Стеклова функция | Стеклова функция (далее С) функция, определяемая для данной функции f (x) равенством
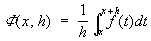 , ,
где h настолько мало, что интервал (x, х + h) лежит в области определения функции f (x). С применяются для сглаживания данной функции, т.к. если функция f (x) непрерывна, то Ф (х, h) имеет на одну производную больше, чем f (x). При этом limФ (х, h) = f (x), то есть С могут применяться для приближения непрерывных функций более гладкими. Если функция f (x) интегрируема, то функция Ф (х, h) непрерывна. С введены В. А. Стекловым в 1903 и применялись им для решения многих вопросов в математической физике. С могут быть определены и для нескольких переменных.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 14:37:28
|

|

|
 |
|

|
 |
 |
 |
|