
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Статистических решений теория | Статистических решений теория (далее С) часть математической статистики и игр теории, позволяющая единым образом охватить такие разнообразные задачи, как статистическая проверка гипотез, построение статистических оценок параметров и доверительных границ для них, планирование эксперимента и др. В основе С лежит предположение, что распределение вероятностей наблюдаемой случайной величины X принадлежит некоторому априори данному множеству 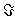 . Основная задача С состоит в отыскании наилучшего статистического решения или решающего правила (функции) d = d (x), позволяющего по результатам наблюдений х над Х судить об истинном (но неизвестном) распределении . Для сравнения достоинств различных решающих правил вводят в рассмотрение функцию потерь (, d (x)), представляющую убыток от принятия решения d (x) (из заданного множества D), когда истинное распределение есть . Естественно было бы считать решающее правило d* = d*(x) наилучшим, если средний риск r (, d*) = M (, d (X)) (M - усреднение по распределению ) не превышает r (, d) для любого Î . Основная задача С состоит в отыскании наилучшего статистического решения или решающего правила (функции) d = d (x), позволяющего по результатам наблюдений х над Х судить об истинном (но неизвестном) распределении . Для сравнения достоинств различных решающих правил вводят в рассмотрение функцию потерь (, d (x)), представляющую убыток от принятия решения d (x) (из заданного множества D), когда истинное распределение есть . Естественно было бы считать решающее правило d* = d*(x) наилучшим, если средний риск r (, d*) = M (, d (X)) (M - усреднение по распределению ) не превышает r (, d) для любого Î 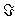 и любого решающего правила d = d (x). Однако такое "равномерно наилучшее" решающее правило в большинстве задач отсутствует, в связи с чем наибольший интерес в С представляет отыскание т. н. минимаксных и бейесовских решений. Решение и любого решающего правила d = d (x). Однако такое "равномерно наилучшее" решающее правило в большинстве задач отсутствует, в связи с чем наибольший интерес в С представляет отыскание т. н. минимаксных и бейесовских решений. Решение 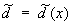 называется минимаксным, если называется минимаксным, если
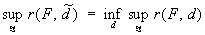
Решение 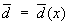 называется бейесовским (относительно заданного априорного распределения n на множестве называется бейесовским (относительно заданного априорного распределения n на множестве 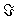 ), если для всех решающих правил d ), если для всех решающих правил d
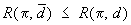 , ,
где
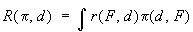
между минимаксными и бейесовскими решениями существует тесная связь, заключающаяся в том, что в весьма широких предположениях о данных задачи минимаксное решение является бейесовским относительно "наименее благоприятного" априорного распределения p.
Лит.: Вальд А., Статистические решающие функции, в сборнике: Позиционные игры, М., 1967: Леман Э., Проверка статистических гипотез, пер. с англ., М., 1964.
А. Н. Ширяев.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:30:05
|

|

|
 |
|

|
 |
 |
 |
|