Средние

Средние (далее С) средние значения, числовая характеристика группы чисел или функций. 1)      Средним для данной группы чисел x1, x2,..... xn называется любое число, заключенное между наименьшим и наибольшим из них. Наиболее употребительными С являются: арифметическое среднее 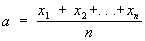 ,   геометрическое среднее 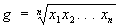,   гармоническое среднее 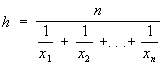  ,   квадратичное среднее 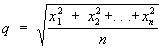  .   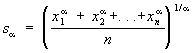Если все числа xi (i = l,2,..., n) положительны, то можно для любого a ¹ 0 определить степенное С     частными случаями которого являются арифметическое, гармоническое и квадратичное С, именно: s (а равняется a, h и q соответственно при a = 1, —1 и 2. При a ® 0 степенное С, sa стремится к геометрическому С, так что можно считать s0 = g. Важную роль играет неравенство sa £ sb, если a £ b, в частности   h £ g £ a £ q.   Арифметическое и квадратичное С находят многочисленные применения в теории вероятностей, математической статистике, при вычислении по методу наименьших квадратов и др. Указанные выше С могут быть получены из формулы 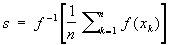  ,   где f-1(h) — функция, обратная к f (x) (см. Обратная функция), при соответствующем подборе функции f (x). Так, арифметическое С получается, если f(x) = x, геометрическое С — если f (x) = log x, гармоническое С — если f (x) = 1/x, квадратичное С — если f (x) = x2.   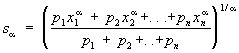Наряду со степенными С рассматривают взвешенные степенные С     в частности при a = 1, 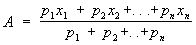  ,   которые переходят в обыкновенные степенные С при р1 = р2 =... = pn. Взвешенные С особенно важны при математической обработке результатов наблюдений (см. Наблюдений обработка), когда различные наблюдения производятся с разной точностью (с разным весом).   2) Арифметико-геометрическое среднее. Для пары положительных чисел а и b составляются арифметическое С a1 и геометрическое С g1. Затем для пары a1, g1 снова находятся арифметическое С a2 и геометрическое С g2 и т.д. Общий предел последовательностей an и gb, существование которого было доказано К. Гауссом, называется арифметико-геометрическим С чисел а и b; он важен в теории эллиптических функций.   3) Средним значением функции называется любое число, заключенное между наименьшим и наибольшим ее значениями. В дифференциальном и интегральном исчислении имеется ряд "теорем о среднем", устанавливающих существование таких точек, в которых функция или ее производная получает то или иное среднее значение. Наиболее важной теоремой о С в дифференциальном исчислении является теорема Лагранжа (теорема о конечном приращении): если f (x) непрерывна на отрезке (а, b) и дифференцируема в интервале (а, b), то существует точка с, принадлежащая интервалу (а, b), такая, что f (b) — f (a) = (b—a) f`(c). В интегральном исчислении наиболее важной теоремой о С является следующая: если f (x) непрерывна на отрезке (а, b), а j(x) сохраняет постоянный знак, то существует точка с из интервала (а, b) такая, что 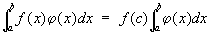  .   В частности, если j(x) = 1, то 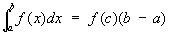  .   Вследствие этого под средним значением функции f (x) на отрезке (а, b) обычно понимают величину 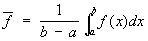  .   Аналогично определяют среднее значение функции нескольких переменных в некоторой области.