
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Спектральное разложение (случайной функции) | Спектральное разложение (далее С)случайной функции, разложение случайной функции (в частности, случайного процесса) в ряд или интеграл по той или иной специальной системе функций такое, что коэффициенты этого разложения представляют собой взаимно некоррелированные случайные величины. Наиболее известный класс С(случайной функции) случайных функций — представления стационарных случайных процессов Х (t) в виде интеграла Фурье — Стилтьеса
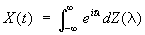 , ,
где Z(l) — случайная функция с некоррелированными приращениями. Существование такого С(случайной функции) показывает, что стационарный случайный процесс всегда можно рассматривать как наложение некоррелированных друг с другом гармонических колебаний различных частот со случайными фазами и амплитудами. С(случайной функции) аналогичного вида, но с заменой гармонических колебаний n-мерными плоскими волнами, имеет место и для однородных случайных полей в n-мерном пространстве. Другой тип С(случайной функции) случайных функций — это разложение случайного процесса X(t), заданного на конечном отрезке оси (или, более общо, случайной функции X(t), заданной на ограниченной области n-мерного пространства), в ряд вида
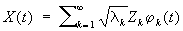 , ,
где jk(t) и lk — собственные функции и собственные значения интегрального оператора в функциональном пространстве с ядром, равным корреляционной функции случайного процесса (или функции) X(t), a Zk, k = 1, 2,..., — последовательность попарно некоррелированных случайных величин единичной дисперсии. С(случайной функции) специального вида имеют место также для однородных и изотропных случайных полей в евклидовых пространствах и для однородных полей на пространствах с группой преобразований, отличных от евклидова пространства.
Лит.: Яглом А. М., Спектральные представления для различных классов случайных функций, в кн.; Труды 4-го Всесоюзного математического съезда, т. 1, Л., 1963, с. 250—73: Гихман И. И., Скороход А. В., Теория случайных процессов, т.1, М., 1971.
А. М. Яглом. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 03.02.2026 12:41:31
|

|

|
 |
|

|
 |
 |
 |
|