|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Собственные векторы | Собственные векторы (далее С) линейного преобразования, векторы, которые при этом преобразовании не меняют своего направления, а только умножаются на скаляр. Например, С преобразования, составленного из вращении вокруг некоторой оси и сжатия к перпендикулярной ей плоскости, служат векторы, направленные по этой оси. Координаты х1, х2,..., xn С линейного преобразования n-мерного пространства с матрицей преобразования ||aik|| удовлетворяют системе однородных линейных уравнений 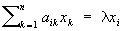 ,  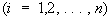, где l — одно из собственных значений этой матрицы. Если матрица преобразования самосопряженная (см. Самосопряженная матрица), то С взаимно перпендикулярны. При самосопряженном преобразовании сфера переходит в эллипсоид, главными осями которого являются С преобразования.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.02.2025 12:04:21
|
|
|
|
|
|
|
|
|
|
|
