
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Сложная функция | Сложная функция (далее С), функция от функции. Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то есть u = j(х), то у является С от х, то есть y = f ((x)), определенной для тех значений х, для которых значения j(х) входят в множество определения функции f (u). В таком случае говорят, что у является С независимого аргумента х, а u - промежуточным аргументом. Например, если у = u2, u = sinx, то у = sin2х для всех значений х. Если же, например, у = 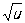 , u = sinx, то у = , u = sinx, то у = 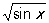 , причем, если ограничиваться действительными значениями функции, С у как функция х определена только для таких значений х, для которых sin ³ 0, то есть для , причем, если ограничиваться действительными значениями функции, С у как функция х определена только для таких значений х, для которых sin ³ 0, то есть для 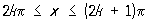 , где k = 0, ± 1, ± 2,... , где k = 0, ± 1, ± 2,...
Производная С равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимому аргументу. Это правило (цепное правило) распространяется на С с двумя, тремя и т. д. промежуточными аргументами: если у = f (u1), u1 = j(u2),..., uk-1 = jk-1(uk), uk = jk (x), то
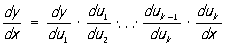
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.02.2026 13:08:19
|

|

|
 |
|

|
 |
 |
 |
|