
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Скалярное произведение | Скалярное произведение (далее С) векторов а и b, скаляр, равный произведению длин этих векторов и косинуса угла между ними; обозначается (а, b) (или ab). Например, работа постоянной силы вдоль прямолинейного пути равна (, ). Свойства С: 1) (а, b) = (b, а), 2) (aа, b) = a(а, b) (a — скаляр), 3) (a, b + c)= (a, b) + (а, с), 4) (a, a) > 0, если а ¹ 0, и (а, а) = 0, если а = 0.
Длина вектора а равна 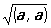 . Если (а, b) = 0, то либо а = 0, либо b = 0, либо a ^ b. Если а = (a1, a2, a3) и b = (b1, b2, b3), то (а, b) = a1 b1 + a2b2 + a3b3 (в прямоугольных декартовых координатах). Понятие "С" обобщают на n-мерные векторные пространства, где равенство (а, b) = . Если (а, b) = 0, то либо а = 0, либо b = 0, либо a ^ b. Если а = (a1, a2, a3) и b = (b1, b2, b3), то (а, b) = a1 b1 + a2b2 + a3b3 (в прямоугольных декартовых координатах). Понятие "С" обобщают на n-мерные векторные пространства, где равенство (а, b) = 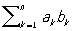 принимают за определение С. и. и с помощью так определенного С вводят геометрическое понятия длины вектора, угла между векторами и т. д. Бесконечномерное линейное пространство, в котором определено С и выполнена аксиома полноты относительно нормы принимают за определение С. и. и с помощью так определенного С вводят геометрическое понятия длины вектора, угла между векторами и т. д. Бесконечномерное линейное пространство, в котором определено С и выполнена аксиома полноты относительно нормы 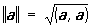 (см. Полное пространство), называют гильбертовым пространством. Гильбертовы пространства играют важную роль в функциональном анализе и квантовой механике. Для векторных пространств над полем комплексных чисел условие 1) заменяют условием (а, b) = (см. Полное пространство), называют гильбертовым пространством. Гильбертовы пространства играют важную роль в функциональном анализе и квантовой механике. Для векторных пространств над полем комплексных чисел условие 1) заменяют условием (а, b) =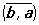 и С определяют как и С определяют как 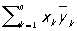 . .
Векторы а и b можно рассматривать как кватернионы a1i + a2j + a3k и b1i + b2j + b3k. Тогда их С равно взятой с обратным знаком скалярной части произведения этих кватернионов (а векторное произведение — векторной части). |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 18:10:37
|

|

|
 |
|

|
 |
 |
 |
|