|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Сингулярные интегральные уравнения | Сингулярные интегральные уравнения (далее С) интегральные уравнения с ядрами, обращающимися в бесконечность в области интегрирования так, что соответствующий несобственный интеграл, содержащий неизвестную функцию, расходится и заменяется своим главным значением по Коши. Примером С может служить следующее уравнение с т. н. ядром Гильберта:
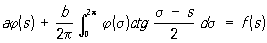
решением которого является функция
 ,
 ,  ,
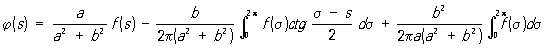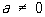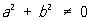где первый интеграл также понимается в смысле главного значения по Коши.
Хорошо изученным общим классом С являются уравнения с ядром Коши вида:
 , (*)
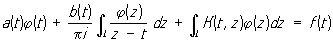где a (t), b (t), f (t) - заданные непрерывные функции точки t пути интегрирования L (который может состоять из конечного числа гладких самонепересекающихся замкнутых или незамкнутых кривых с непрерывной кривизной) в комплексной плоскости; сингулярный интеграл
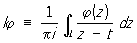
понимается как предел при e ® 0 интеграла 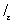 j по пути Le, который получается из L после удаления симметричной относительно точки t дуги длины 2e. Ядро (t, z) предполагается принадлежащим к одному из тех классов, которые рассматриваются в теории несингулярных интегральных уравнений. К С вида (*) приводят многие задачи теории аналитических функций, теории упругости, гидродинамики и др.
Исследование С (*) опирается на свойства сингулярного интеграла j, которые зависят от предположений, делаемых относительно j. Подробно С исследованы в пространстве непрерывных функций j и в пространстве функций, интегрируемых с квадратом. Основное свойство сингулярного интеграла j выражается равенством 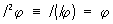 , справедливым для широкого класса функций.
Многие результаты теории С почти без изменений переносятся на системы С, которые можно записать в виде (*), если под а и b понимать матричные функции, а под f и j - векторы (одноколонные матрицы). Теория обобщается также на случай системы С с разрывными коэффициентами и кусочно-гладким путем интегрирования. Изучены также некоторые классы С в многомерных областях.
С впервые (начало 20 в.) встретились в исследованиях А. Пуанкаре (по теории приливов) и Д. Гильберта (по краевым задачам). Ряд важных свойств С установил нем. математик Ф. Нетер. Для разработки теории С важное значение имели работы Т. Карлемана и И. И. Привалова. Наиболее полные результаты получены сов. учеными (Н. И. Мусхелишвили, И. Н. Векуа, В. Д. Купрадзе и др.).
Лит.: Мусхелишвили Н. И., С. Граничные задачи теории функций и некоторые их приложения к математической физике, 3 изд., М., 1968; Векуа Н. П., Системы сингулярных интегральных уравнений и некоторые граничные задачи, 2 изд., М., 1970.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
