
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Симпсона формула | Симпсона формула (далее С) формула для приближенного вычисления определенных интегралов, имеющая вид:
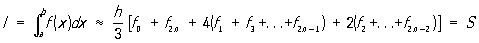 , ,
где h = (b - а)/2n; fi, = f (a + ih), i = 0, 1, 2,..., 2n. С называют иногда формулой парабол, т. к. вывод этой формулы основан на замене подынтегральной функции f (x) на каждом из отрезков (a + 2hk, а + 2h (k + 1)), k = 0, 1,..., n - 1, соответствующим интерполяционным многочленом второй степени (см. Интерполяционные формулы); геометрически это означает, что кривая, описываемая уравнением у = f (x), заменяется близкой к ней кривой, состоящей из отрезков парабол. Погрешность, возникающая в результате применения С, равна
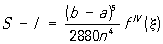 , ,
где а £ x £ b. Если подынтегральная функция f (x) - многочлен степени m £ 3, то С является не приближенной, а точной, так как в этом случае f (x) º 0.
С названа по имени Т. Симпсона, получившего ее в 1743, хотя эта формула была известна ранее, например Дж. Грегори (1668).
О других формулах для приближенного вычисления определенных интегралов см. в ст. Приближенное интегрирование.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 03.02.2026 13:00:12
|

|

|
 |
|

|
 |
 |
 |
|