
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Симметрическая матрица | Симметрическая матрица (далее С)квадратная матрица = llsikll, в которой любые два элемента, симметрично расположенные относительно главной диагонали, равны между собой: sik = ski (i, k = 1,2,..., n). Симметрическая матрица часто рассматривается как матрица коэффициентов некоторой квадратичной формы; между теорией Симметрическая матрица и теорией квадратичных форм существует тесная связь.
Спектральные свойства Симметрическая матрица с действительными элементами: 1) все корни l1, l2,..., ln характеристического уравнения Симметрическая матрица действительны; 2) этим корням соответствуют n попарно ортогональных собственных векторов Симметрическая матрица (n — порядок Симметрическая матрица). Симметрическая матрица с действительными элементами всегда представима в виде: "= ODO-1
где О ортогональная матрица, а
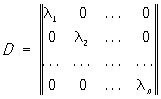 . .
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 13:07:28
|

|

|
 |
|

|
 |
 |
 |
|