
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Автоморфная функция | Автоморфная функция (далее А) (от авто... и греческого morphē - вид) (матем.), аналитическая функция, значения которой не изменяются, если ее аргумент подвергается некоторым дробно линейным преобразованиям. К А относятся периодические функции и, в частности, эллиптические функции.
Так, например, если указанные преобразования - целые и имеют вид: z` = z + w, где w - комплексное число, отличное от нуля, то получаются А, характеризуемые уравнением f (z + w) = f (z), т. е. периодические функции с периодом w. В этом примере преобразованием, не изменяющим функции, является сдвиг плоскости на вектор w. Очевидно, что тот же сдвиг, повторенный сколько угодно раз, также не изменяет функции. В результате получается группа линейных преобразований z` = z + nw (n = 0, ±1, ±2,...), не изменяющих f (z). В общем случае пусть Г - некоторая группа дробно линейных преобразований;
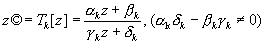
и G - область, которая каждым из этих преобразований отражается сама на себя. Тогда функция f, однозначная и аналитическая в области G, является А (по отношению к данной группе Г), если f (Tk (z)) = f (z), (k = 1, 2...). Наиболее важен случай, когда G есть круг или полуплоскость. Такую область можно рассматривать как изображение плоскости Лобачевского (см. Лобачевского геометрия), а преобразования группы Г - как движения в плоскости Лобачевского. Соответствующие А можно рассматривать как такое обобщение периодических функций, при котором сдвиги в евклидовой плоскости заменены движениями в плоскости Лобачевского. Эта точка зрения, развитая А. Пуанкаре, обеспечила успех в построении общей теории А (до А. Пуанкаре существенные результаты теории А получены Ф. Клейном). Вообще, вся теория А, в ее современном состоянии, представляет замечательный пример плодотворности геометрических идей Н. И. Лобачевского в их применении к задачам математического анализа и теории функций.
К общим А, помимо вопросов конформного отображения, приводит также теория линейных дифференциальных уравнений, изучение алгебр, кривых порядка выше четвертого (см. Алгебраическая геометрия), решение алгебраических уравнений (например, решение общего уравнения пятой степени с одним неизвестным получается посредством А) и т. д.
Лит.: Форд Л. ., Автоморфные функции, пер. с англ., М.- Л., 1936; Клейн Ф., Лекции о развитии математики в 19 столетии, пер. с нем., ч. 1, М.- Л., 1937, гл. 8; Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, 2 изд., М.- Л., 1950; его же, Однозначные аналитические функции. Автоморфные функции, М., 1961. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:37:40
|

|

|
 |
|

|
 |
 |
 |
|