|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Самосопряженное дифференциальное уравнение | Самосопряженное дифференциальное уравнение (далее С) уравнение, имеющее те же решения, что и сопряженное с ним (см. Сопряженные дифференциальные уравнения). Обыкновенное С четного порядка 2m имеет вид
 ,
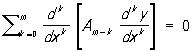а нечетного порядка 2m — 1 имеет вид
 ,
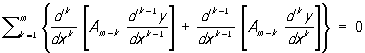где Ai — функции от x. Понятие С играет большую роль в теории дифференциальных уравнений, обыкновенных и с частными производными. При некоторых краевых условиях левая часть С определяет самосопряженный дифференциальный оператор. Наиболее важны в приложениях С второго порядка.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 27.02.2025 23:01:59
|
|
|
|
|
|
|
|
|
|
|
