
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Римана сфера | Римана сфера (далее Р), одно из возможных геометрических изображений совокупности комплексных чисел, введенное Б. Риманом. Комплексное число
z = х + iy = r (cos j + i sin j) = reij
можно изображать точками на плоскости (комплексной числовой плоскости) с декартовыми координатами х, у или полярными r, j. Для построения Р проводится сфера, касающаяся комплексной числовой плоскости в начале координат; точки комплексной числовой плоскости отображаются на поверхность сферы с помощью стереографической проекции. В этом случае каждое комплексное число изображается соответствующей точкой сферы; последняя и называется сферой Римана. Число О изобразится при этом южным полюсом Р; числа с одинаковым аргументом j = const (лучи комплексной числовой плоскости) изобразятся меридианами, а числа с одинаковым модулем r = const (окружности комплексной числовой плоскости) - параллелями Р Северному полюсу Р не соответствует никакая точка комплексной числовой плоскости. В целях сохранения взаимной однозначности соответствия между точками комплексной числовой плоскости и Р на плоскости вводят "бесконечно удаленную точку", которую считают соответствующей северному полюсу и обозначают z = ¥ Т. о., на комплексной числовой плоскости имеется одна бесконечно удаленная точка, в отличие от проективной плоскости.
Если в пространстве ввести прямоугольную систему координат x, h, z так, что оси x и h совпадают, соответственно, с осями х и у, то точке x + iy комплексной числовой плоскости соответствует точка
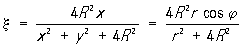 , ,
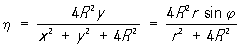 , ,
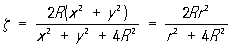
Р (уравнение которой 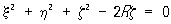 ). ).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 22:54:10
|

|

|
 |
|

|
 |
 |
 |
|