
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Риккати уравнение | Риккати уравнение (далее Р) обыкновенное дифференциальное уравнение 1-го порядка вида
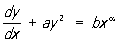 , (*) , (*)
где а, b, а — постоянные. Это уравнение впервые исследовалось Я. Риккати (1724); отдельные частные случаи рассматривались раньше. Д. Бернулли установил (1724—25), что уравнение (*) интегрируется в элементарных функциях, если а = — 2 или а = — 4kl (2k — 1), где k — целое число. Как доказал Ж. Лиувилль (1841), при других значениях а решение уравнения (*) нельзя выразить в квадратурах от элементарных функций; общее решение его может быть записано с помощью цилиндрических функций. Дифференциальное уравнение
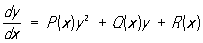 , ,
где Р (х), Q (x), R (x) — непрерывные функции, называется общим Р (в отличие от него уравнение (*) называется специальным Р). При Р (х) = 0 общее Р является линейным дифференциальным уравнением, при R (x) = 0 — так называемым Бернулли уравнением, которые интегрируются в конечном виде. Изучены также другие случаи интегрируемости общего Р
Лит.: Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 4 изд., М., 1971.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 21:03:29
|

|

|
 |
|

|
 |
 |
 |
|