
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Рекурсивные функции | Рекурсивные функции (далее Р) (от позднелатинского recursio - возвращение), название, закрепившееся за одним из наиболее распространенных вариантов уточнения общего понятия арифметического алгоритма, т.е. такого алгоритма, допустимые исходные данные которого представляют собой системы натуральных чисел, а возможные результаты применения являются натуральными числами. Р были введены в 30-х гг. 20 в. С. К. Клини, в свою очередь основывавшимся на исследованиях К. Геделя, Ж. Эрбрана и др. математиков.
Каждая Р задается конечной системой равенств точно охарактеризованного типа в том смысле, что ее значения вычисляются с помощью этой системы равенств по точно формулируемым правилам, причем таким образом, что в итоге для вычисления значений заданной Р получается алгоритм определенного типа.
Арифметические функции, для вычисления значений которых имеются какие-либо алгоритмы, принято называть вычислимыми. Вычислимые функции играют в математике важную роль. Вместе с тем, если понятию алгоритма здесь не будет придан точный смысл, то и само понятие вычислимой функции окажется несколько расплывчатым. Р уже в силу самого характера своего определения оказываются вычислимыми. В известном смысле верно и обратное: имеются серьезные основания считать, что математическое по своему характеру понятие рекурсивности является точным эквивалентом несколько расплывчатого понятия вычислимости. Предложение считать понятие вычислимости совпадающим по объему с понятием рекурсивности известно в теории Р под названием тезиса Черча по имени американского математика А. Черча, впервые (в 30-х гг. 20 в.) сформулировавшего и обосновавшего это предложение. Принятие тезиса Черча позволяет придать понятию вычислимой арифметической функции точный математический смысл и подвергнуть это понятие изучению при помощи точных методов.
Р являются частичными функциями, т. е. функциями, не обязательно всюду определенными. Чтобы подчеркнуть это обстоятельство, часто в качестве синонима используют термин "частично рекурсивные функции". Р, определенные при любых значениях аргументов, называют общерекурсивными функциями.
Определению Р может быть придана следующая форма. Фиксируется небольшое число чрезвычайно простых исходных функций, вычислимых в упомянутом выше интуитивном смысле (функция, тождественно равная нулю, функция прибавления единицы и функции, выделяющие из системы натуральных чисел член с данным номером); фиксируется небольшое число операций над функциями, переводящих вычислимые функции снова в вычислимые (операторы подстановки, примитивной рекурсии и минимизации). Тогда Р определяются как такие функции, которые можно получить из исходных в результате конечного числа применений упомянутых выше операций.
Оператор подстановки сопоставляет функции f от n переменных и функциям g1, . . ., gn от m переменных функцию h от m переменных такую, что для любых натуральных чисел x1, .., xm
h(x1, .., xm) @ f (g1(x1, .., xm), ..., gm(x1, .., xm*(
(здесь и ниже условное равенство @ означает, что оба выражения, связываемые им, осмыслены одновременно и в случае осмысленности имеют одно и то же значение).
Оператор примитивной рекурсии сопоставляет функциям f от n переменных и g от n + 2 переменных функцию h от n + 1 переменных такую, что для любых натуральных чисел x1, .. .., xn, y
h(x1, .., xn ,0) @ f(x1, .., xn),
h(x1, .., xn, y + 1) @ g(x1, .., xn, y, h(x1, .., xn, y *(.
Оператор минимизации сопоставляет функции f от n переменных функцию h от n переменных такую, что для любых натуральных чисел x1, .., xn
h(x1, .., xn) @ f(x1, .., xn-1, y)
где у таково, что f(x1, .., xn-1, y-1) определены и отличны от xn, а f(x1, .., xn, y) определена и равна xn, если же у с указанными свойствами не существует, то значение h(x1, .., xn) считается не определенным.
Важную роль в теории Р играют т. н. примитивно рекурсивные функции - Р, получающиеся из исходных функций в результате конечного числа применений одних лишь операторов подстановки и примитивной рекурсии. Они образуют собственную часть класса общерекурсивных функций. В силу известной теоремы Клини о нормальной форме Р могут быть указаны такие конкретные примитивно рекурсивные функции от одной переменной и Tn от n + 2 переменных, что для любой Р j от n переменных и для любых натуральных чисел x1, . . ., xn имеет место равенство j(x1, ..., xn) @ (y), где у есть наименьшее из чисел z таких, что Tn(j, x1, ..., xn,z) = 0 (здесь j представляет собой т. н. геделев номер функции j - число, которое эффективно строится по системе равенств, задающей функцию j). Из этой теоремы, в частности, вытекает, что для Р от п переменных может быть построена универсальная Р от n+1 переменных, т. е. такая Р Фn, что для любой Р j от n переменных и для любых натуральных чисел x1, . . ., xn имеет место условное равенство
j( x1, . . ., xn) @ Фn(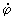 , x1, . . ., xn). , x1, . . ., xn).
Это - один из центральных результатов общей теории Р
Теория Р, являясь частью алгоритмов теории, представляет собой разветвленную математическую дисциплину с собственной проблематикой и с приложениями в др. разделах математики. Понятие "Р" может быть положено в основу конструктивного определения исходных математических понятий. Широкое применение теория Р нашла в математической логике. В частности, понятие примитивно рекурсивной функции лежит в основе первоначального доказательства знаменитой теоремы Геделя о неполноте формальной арифметики, а понятие "Р" в его полном объеме было использовано С. К. Клини для интерпретации интуиционистской арифметики (исследование это составило целую эпоху в области семантики). Аппарат теории Р используется также в теории вычислительных машин и программирования.
Исследования показали, что все известные уточнения общего понятия алгоритма, в том числе Р, взаимно моделируют друг друга и, следовательно, ведут к одному и тому же понятию вычислимой функции. Это обстоятельство служит серьезным доводом в пользу тезиса Черча.
Лит.: Клини С. К., Введение в математику. пер. с англ., М., 1957; Успенский В. А., Лекции о вычислимых функциях, М., 1960; Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; Роджерс Х., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972.
Н. М. Нагорный. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.02.2026 15:04:07
|

|

|
 |
|

|
 |
 |
 |
|