
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Рекуррентная формула | Рекуррентная формула (далее Р) (от лат. recurrens, родительный падеж recurrentis — возвращающийся), формула приведения, формула, сводящая вычисление n-го члена какой-либо последовательности (чаще всего числовой) к вычислению нескольких предыдущих ее членов. Обычно эти члены находятся в рассматриваемой последовательности "недалеко" от ее n-го члена, число их от n не зависит, а n-й член выражается через них достаточно просто. Однако возможны Р и более сложной структуры. Общая проблематика рекуррентных вычислений является предметом теории рекурсивных функций.
Примеры. 1) Последовательность jn — т. н. чисел Фибоначчи — задается формулами:
j0 = 0, j1 = 1, jn+2 = jn+1 + jn (n > 0)
Последняя из них является Р; она позволяет вычислить j2, j3 и дальнейшие члены этой последовательности.
2) Пусть
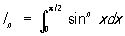
Нетрудно показать, что для n ³ 2 выполняется соотношение
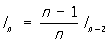 . .
Это — Р, сводящая вычисление n к вычислению /0 или l1 в зависимости от четности n.
Р обычно дает удобную вычислительную схему для нахождения членов последовательности друг за другом. Однако иногда, исходя из Р, стремятся получить "явное" выражение для n-го члена последовательности, описываемой этой Р Так, в случае чисел Фибоначчи
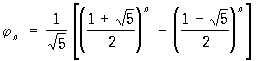 . .
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 09.02.2026 13:14:39
|

|

|
 |
|

|
 |
 |
 |
|