
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Регулярная точка | Регулярная точка (далее Р) (от лат. regularis - правильный), правильная точка, математический термин, употребляющийся в различных смыслах. Р функции f(z) комплексного переменного z = x + iy (i =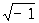 ) - точка z0 = x0 + iy0, в некоторой окрестности ïz - z0ï < r которой функция f(z) однозначна и представима в виде ряда: f(z) = ) - точка z0 = x0 + iy0, в некоторой окрестности ïz - z0ï < r которой функция f(z) однозначна и представима в виде ряда: f(z) = 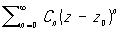 (n - постоянные). В аналитической теории дифференциальных уравнений особая точка называется регулярной для уравнения (n - постоянные). В аналитической теории дифференциальных уравнений особая точка называется регулярной для уравнения 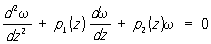 , если она является полюсом порядка не выше k для коэффициентов pk(k = 1, 2). Точка x0 называется Р разрыва функции f(x), если f(x0) = , если она является полюсом порядка не выше k для коэффициентов pk(k = 1, 2). Точка x0 называется Р разрыва функции f(x), если f(x0) = 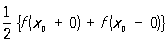 , где f(x0 - 0) и f(x0 + 0) - пределы функции, соответственно, слева и справа. Это понятие находит применение в теории рядов Фурье. , где f(x0 - 0) и f(x0 + 0) - пределы функции, соответственно, слева и справа. Это понятие находит применение в теории рядов Фурье.
Лит.: Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М., 1969; Маркушевич А. И., Краткий курс теории аналитических функций, 3 изд., М., 1966.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:59:18
|

|

|
 |
|

|
 |
 |
 |
|