
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Регулирование автоматическое | Регулирование автоматическое (далее Р) (от нем. regulieren — регулировать, от лат. regula — норма, правило), поддержание постоянства (стабилизация) некоторой регулируемой величины, характеризующей технический процесс, либо ее изменение по заданному закону (программное регулирование) или в соответствии с некоторым измеряемым внешним процессом (следящее регулирование), осуществляемое приложением управляющего воздействия к регулирующему органу объекта регулирования; разновидность автоматического управления. При Р управляющее воздействие u(t) обычно является функцией динамической ошибки — отклонения e(t) регулируемой величины х(t) от ее заданного значения x0(t): e(t) = x0(t) — х(t) (принцип Ползунова — Уатта регулирования по отклонению, или принцип обратной связи) (рис., а). Иногда к Р относят также управление, при котором u(t) вырабатывается (устройством компенсации) в функции возмущающего воздействия f (нагрузки) на объект (принцип Понселе регулирования по возмущению) (рис., б), и комбинированное регулирование по отклонению и возмущению (рис., б).
Для осуществления Р к. объекту подключается комплекс устройств, представляющих собой в совокупности регулятор. Объект и регулятор образуют систему автоматического регулирования (CAP). САР по отклонению является замкнутой (см. Замкнутая система управления), по возмущению — разомкнутой (см. Разомкнутая система управления). Математическое выражение функциональной зависимости желаемого (требуемого) управляющего воздействия u0(t) от измеряемых регулятором величин называется законом, или алгоритмом, регулирования. Наиболее часто применяемые законы Р: П — пропорциональный (статический), u0 = ke, И — интегральный ( 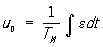 ; ПИ — пропорционально-интегральный (изодромный), ; ПИ — пропорционально-интегральный (изодромный), 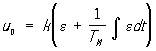 , ПИД — пропорционально-интегральный с производной, , ПИД — пропорционально-интегральный с производной, 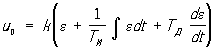 ; здесь k — коэффициет усиления регулятора, Ти и Тд — постоянные времени интегрирования и дифференцирования. Фактическое воздействие u(t) отличается от u0(t) вследствие инерционности регулятора. CAP является динамической системой, процессы в которой описываются дифференциальными, дифференциально-разностными и т. п. уравнениями. ; здесь k — коэффициет усиления регулятора, Ти и Тд — постоянные времени интегрирования и дифференцирования. Фактическое воздействие u(t) отличается от u0(t) вследствие инерционности регулятора. CAP является динамической системой, процессы в которой описываются дифференциальными, дифференциально-разностными и т. п. уравнениями.
САР может находиться в состоянии равновесия, в ней могут протекать установившиеся и переходные процессы, количественные характеристики которых изучает теория автоматического регулирования (ТАР). В статических системах регулирования установившаяся погрешность (ошибка ) eст при постоянной нагрузке (на объект) зависит от величины последней. Для повышения статической точности увеличивают коэффициент усиления регулятора k, но при достижении им некоторого критического значения kkp система обычно теряет устойчивость. Введение в регулятор интегрирующих элементов позволяет получить астатическую систему регулирования, в которой при любой постоянной нагрузке статическая ошибка отсутствует. ТАР изучает условия устойчивости, показатели качества процесса регулирования (динамическую и статическую точность, время регулирования, колебательность системы, степень и запасы устойчивости и т. п.) и методы синтеза CAP, т. е. определения структуры и параметров корректирующих устройств, вводимых в регулятор для повышения устойчивости и обеспечения требуемых показателей качества Р
Наиболее полно разработана ТАР линейных систем, в которой применяются аналитические и частотные методы исследования. Малые отклонения от равновесных состояний в непрерывных нелинейных системах Р исследуются посредством линеаризации исходных уравнений. Процессы при больших отклонениях и специфических особенности; нелинейных CAP (предельные циклы, автоколебания, захватывание, скользящие режимы и т. п.) изучаются методами фазового пространства. Для изучения периодических режимов также применяют приближенные методы малого параметра, гармония, баланса и др. Устойчивость при больших отклонениях исследуется вторым (прямым) методом Ляпунова и методом абсолютной устойчивости, разработанным : В. М. Поповым (Румыния). Специальный раздел ТАР посвящен Р при случайных воздействиях.
С 50-х гг. 20 в. развиваются теория инвариантных CAP, обеспечивающих независимость х(t) от возмущений, и теория многосвязных CAP, в которых многие величины связаны через регулируемый объект. В таких CAP часто вводят дополнительные связи между регуляторами в целях получения определенных свойств, в частности автономности (независимости процессов регулирования отдельных величин). В 60-х гг. получила развитие и применение теория систем с переменной структурой, особенно эффективных при работе в условиях больших изменений параметров системы и среды, т. к. переходные процессы в них определяются свойствами управляющего устройства и мало зависят от параметров объекта регулирования и среды.
Особое место в ТАР занимают дискретные системы Р, в которых осуществляется квантование сигнала. Из них наиболее изучены импульсные системы (с квантованием по времени), релейные системы (с квантованием по уровню) и цифровые системы (с квантованием по времени и уровню). Частный вид релейных систем — двухпозиционные регуляторы, в которых регулирующий орган может занимать лишь одно из двух крайних положений.
История развития Р Даты изобретения первых регулирующих устройств, так же как и имена их изобретателей, не установлены. Например, поплавковый регулятор уровня водяных часов, основанный на принципе регулирования по отклонению, был известен арабам еще в начале н. э. На мукомольных мельницах в средние века применялись центробежные маятники для регулирования частоты вращения жерновов. Однако первыми регуляторами, получившими широкое практическое применение в промышленности, стали регулятор питания котла паровой машины И. И. Ползунова (1765) и центробежный регулятор частоты вращения паровой машины Дж. Уатта (1784).
Первые регуляторы осуществляли прямое регулирование, при котором измерительный орган непосредственно воздействовал на регулирующий орган. Такое Р было возможно только на машинах малой мощности, где для перемещения регулирующих органов (рычага, колеса) не требовалось больших затрат энергии. В 1873 французский инженер Ж. Фарко впервые осуществил непрямое Р, введя в цепь регулирования усилитель — гидравлический сервомотор с жесткой обратной связью. Это дало возможность не только повысить мощность воздействия регулятора, но и получить более гибкие алгоритмы Р В 1884 появился регулятор непрямого действия с дополнительной релейной обратной связью, действовавшей до тех пор, пока отклонение было отлично от нуля. Затем релейная связь была заменена непрерывной дифференциальной связью, получившей название изодромной.
Со 2-й половины 19 в. Р применяется в самых различных технических устройствах— паровых котлах, компрессорных установках, электрических машинах и др. К этому же периоду относится и становление науки о Р В статье Дж. К. Максвелла "О регулировании" (1868) впервые рассмотрена математическая задача об устойчивости линейной CAP. Трудом И. А. Вышнеградского "О регуляторах прямого действия" (1877) заложена основа ТАР как новой научно-технической дисциплины. Дальнейшее ее развитие и систематическое изложение дано А. Стодолой, Я. И. Грдиной и Н. Е. Жуковским.
Новый этап в развитии Р наступил с применением в регуляторах электронных элементов, в частности вычислительных устройств, что существенно расширило возможность усовершенствования алгоритмов регулирования введением воздействий по высшим производным, интегралам и более сложным функциям. Преимущества электронных регуляторов особенно проявились в самонастраивающихся системах, первыми из которых были экстремальные регуляторы: регулятор топки парового котла (1926), электрический регулятор кпд (1940), авиационные регуляторы (1944). Однако подобные регуляторы применяют лишь в простейших случаях, например для поддержания экстремума функции одной переменной. В более сложных САР целесообразно разделить систему регулирования на две части: вычислительное устройство, определяющее оптимальную настройку регулятора, и собственно регулятор. В сложных системах управления Р используется лишь на низшей ступени иерархического управления — регуляторы воздействуют непосредственно на управляемый объект, являясь исполнителями команд ЭВМ (или операторов), находящихся на более высоких ступенях управления.
Лит.: Теория автоматического регулирования, под ред. В. В. Солодовникова, книга 1—3, М., 1967—69; Воронов А. А., Основы теории автоматического управления, ч. 1—3, М. — Л., 1965—70; Заде Л., Дезоер Ч., Теория линейных систем. Метод пространства состояний, пер. с англ., М., 1970; Бесекерский В. А., Попов Е, П., Теория систем автоматического регулирования, М., 1972; Сю Д., Мейер А., Современная теория автоматического управления и ее применение, пер. с англ., М., 1972; Основы автоматического управления, под ред. В. С. Пугачева, 3 изд., М., 1974.
А. А. Воронов.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:59:11
|

|

|
 |
|

|
 |
 |
 |
|