
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Рациональная функция | Рациональная функция (далее Р) функция, получающаяся в результате конечного числа арифметических операций (сложения, умножения и деления) над переменным х и произвольными числами. Р имеет вид:
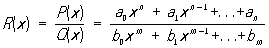 , (1) , (1)
где a0, a1, ..., an и b0, b1, ..., bm (a0 ¹ 0, b0(0)- постоянные, a n и m - неотрицательные целые числа. Р определена и непрерывна для всех значений х, кроме тех, которые являются корнями знаменателя Q (x). Если x - корень кратности k знаменателя Q (x) и одновременно корень кратности r (r ³ k) числителя Р (х), то R (x) имеет в точке x устранимый разрыв; если же r < k, то R (x) имеет в точке x бесконечный разрыв (полюс). Многочлен является частным случаем Р (при m = 0), поэтому многочлены иногда называются целыми Р; всякая Р есть отношение двух многочленов. Др. примером Р может служить дробно-линейная функция.
Если в формуле (1) n < m (m > 0), то Р называется правильной; если же n ³ m, то R (x) может быть представлена в виде суммы многочлена M (x) степени n - m и правильной Р R1(x) = 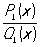 : :
R (x) = М (х) + R1(x),
многочлены М (х) и 1(x) (степень последнего меньше m) однозначно определяются из соотношения
Р (х) = M (x) Q (x) + 1(x)
(формула деления многочлена с остатком).
Из определения Р следует, что функции, получаемые в результате конечного числа арифметических операций над Р и произвольными числами, снова являются Р В частности, Р от Р есть вновь Р Во всех точках, в которых она определена, Р дифференцируема, и ее производная
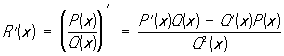
также является Р Интеграл от Р сводится по предыдущему к сумме интеграла от многочлена и интеграла от правильной Р Интеграл от многочлена является многочленом и его вычисление не представляет труда. Для вычисления второго интеграла пользуются формулой разложения правильной Р R1(x) на простейшие дроби:
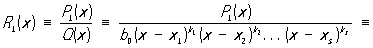 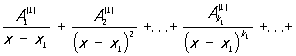 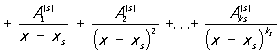
где x1, ..., xs - различные корни многочлена Q (x) соответственно кратностей k1, ..., ks (k1 + ... + ks = m), a 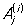 - постоянные коэффициенты. Разложение Р на простейшие дроби (2) определяется однозначно. Если коэффициенты многочленов 1(x) и Q (x) - действительные числа, то комплексные корни знаменателя Q (x) (в случае их существования) распадаются на пары сопряженных, и соответствующие каждой такой паре простейшие дроби в разложении (2) могут быть объединены в вещественные простейшие дроби: - постоянные коэффициенты. Разложение Р на простейшие дроби (2) определяется однозначно. Если коэффициенты многочленов 1(x) и Q (x) - действительные числа, то комплексные корни знаменателя Q (x) (в случае их существования) распадаются на пары сопряженных, и соответствующие каждой такой паре простейшие дроби в разложении (2) могут быть объединены в вещественные простейшие дроби:
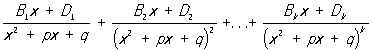
где трехчлен x2 + px + q имеет комплексно-сопряженные корни (4q > p2).
Для определения коэффициентов 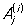 , j и Dj можно воспользоваться неопределенных коэффициентов методом. Интегралы от простейших дробей , j и Dj можно воспользоваться неопределенных коэффициентов методом. Интегралы от простейших дробей
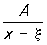 и и 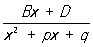
не являются Р. ф
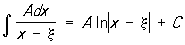 , ,
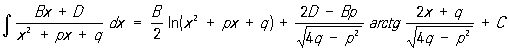
а интегралы от простейших дробей
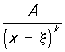 и и 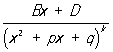
при k > 1 являются: первый - Р, а второй - суммой Р и интеграла такого же вида, как при k = 1. Т. о., интеграл от любой Р (не являющейся многочленом) представляется в виде суммы Р, арктангенсов и логарифмических функций. М. В. Остроградский дал алгебраический метод определения рациональной части интеграла от Р, не требующий ни разложения Р на простейшие дроби, ни интегрирования (см. Остроградского метод).
Р являются весьма важным классом элементарных функций. Рассматриваются также Р нескольких переменных; они получаются в результате конечного числа арифметических операций над их аргументами и произвольными числами. Так,
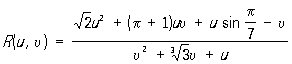
дает пример Р двух переменных u и u.
В середине 20 в. Р нашли широкое применение в вопросах приближения функций (см. Приближение и интерполирование функций).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 01.03.2026 20:37:53
|

|

|
 |
|

|
 |
 |
 |
|