
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Разрыва точка | Разрыва точка (далее Р) значение аргумента, при котором нарушается непрерывность функции (см. Непрерывная функция). В простейших случаях нарушение непрерывности в некоторой точке а происходит так, что существуют пределы
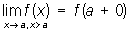
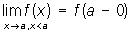
при стремлении x к а справа и слева, но хотя бы один из этих пределов отличен от f (a). В этом случае а называют Р 1-го рода. Если при этом f (a + 0) = f (a -0), то разрыв называется устранимым, так как функция f (x) становится непрерывной в точке а, если положить f (a) = f (a + 0) = f (a - 0). Например, точка а = 0 является точкой устранимого разрыва для функции f (x) = 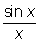 при х ¹ 0 и f (0) = 0, так как для восстановления непрерывности достаточно положить f (0) = 1. Если же скачок d = f (a +0) - f (a - 0) функции f (x) в точке а отличен от нуля, то при любом определении значения f (a) точка а остается Р Примером такой Р служит точка а = 0 для функции f (x) = arctg при х ¹ 0 и f (0) = 0, так как для восстановления непрерывности достаточно положить f (0) = 1. Если же скачок d = f (a +0) - f (a - 0) функции f (x) в точке а отличен от нуля, то при любом определении значения f (a) точка а остается Р Примером такой Р служит точка а = 0 для функции f (x) = arctg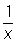 (в этом случае в самой точке а функция может оставаться неопределенной). Р 1-го рода называется правильной, если (в этом случае в самой точке а функция может оставаться неопределенной). Р 1-го рода называется правильной, если
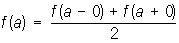
Если хотя бы один из односторонних пределов не существует, то а называется Р 2-го рода (примеры: точка а = 2 для функции 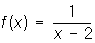 , точка а = 0 для функции , точка а = 0 для функции 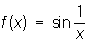 ). ).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 06.02.2026 06:45:39
|

|

|
 |
|

|
 |
 |
 |
|