|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Равносильные уравнения | Равносильные уравнения (далее Р), уравнения, имеющие одно и то же множество корней (в случае кратных корней нужно, чтобы кратности соответствующих корней совпадали). Так, из трех уравнений: 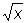 = 2, 3х — 7 = 5, (х — 4)2 = 0, первое и второе — Р, а первое и третье не Р (т.к. кратность корня х = 4 для первого уравнения равна 1, а для третьего равна 2). Если к обеим частям уравнения прибавить один и тот же многочлен от х или умножить обе части на одно и то же число, не равное 0, то получим уравнение, равносильное данному. Например, x2 — x + 1 = x — 1 и x2 — 2x + 2 = 0 — Р (к обеим частям первого прибавлен многочлен: — х + 1); 0,01х2 — 0,37х + 1 = 0 и x2 — 37x + 100 = 0 — также Р (обе части первого умножены на 100). Но если умножить или разделить обе части уравнения на многочлен степени не ниже 1, то полученное уравнение, вообще говоря, не будет равносильным данному. Например, х — 1 = 0 и (х — 1)(х + 1) = 0 — не Р (корень х = — 1 второго не является корнем первого). Понятие "Р" приобретает точный смысл, когда указано поле, в котором лежат корни уравнений. Например, x2 — 1 = 0 и x4 — 1 = 0 — Р в поле действительных чисел (множество корней как для одного, так и для другого состоит из 2 чисел: x1 = 1, x2 = —1). Но они не Р в поле комплексных чисел, т.к. второе имеет еще 2 мнимых корня: x3 = i, x2 = — i. Понятие Р можно применять и к системе уравнений. Например, если Р (х, у) и Q (x, у) — два многочлена от переменных х и у и а, b, с и d — числа (действительные или комплексные), то две системы: Р (х, у) = 0, Q (x, у) = 0 и aP (x, у) + bQ (x, y) = 0, cP (x, y) + dQ (x, y) = 0 равносильны тогда, когда определитель ad — bc ¹ 0.
А. И. Маркушевич. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 25.12.2024 11:06:30
|
|
|
|
|
|
|
|
|
|
|
