|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Равномерные приближения | Равномерные приближения (далее Р)приближения функции, в которых мерой уклонения на данном множестве служит точная верхняя грань модуля разности между данной функцией f (x) и приближающей функцией Р (х). Например, уклонением непрерывной функции Р (х) от непрерывной функции f (x) на отрезке (а, b) будет
 .
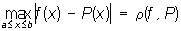Равномерные приближения называются также чебышевскими приближениями по имени П. Л. Чебышева, исследовавшего их в 1854. См. Приближение и интерполирование функций.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 03.02.2025 17:30:26
|
|
|
|
|
|
|
|
|
|
|
