|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Равномерная сходимость | Равномерная сходимость (далее Р)важный частный случай сходимости. Последовательность функций fn (x) (n = 1, 2, ...) называется равномерно сходящейся на данном множестве к предельной функции f (x), если для каждого e > 0 существует такое = (e), что ïf (x) — fn (x)ï < e при n > для всех точек х из данного множества. Например, последовательность функций fn (x) = xn равномерно сходится на отрезке (0, 1/2) к предельной функции f (x) = 0, так как ïf (x) — fn (x)ï £ (1/2) n < e для всех 0 £ x £ 1/2, если только n > ln (1/e)/ln2, но она не будет равномерно сходящейся на отрезке (0, 1), где предельной функцией является f (x) = 0 при 0 £ x < 1 и f (1) = 1, т.к. для любого сколько угодно большого заданного n существуют точки h, удовлетворяющие неравенствам 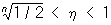 , для которых ïf (h) — fn (h)ï = hn > 1/2. Понятие Равномерная сходимость допускает простую геометрическую интерпретацию: если последовательность функций fn (x) равномерно сходится на некотором отрезке к функции f (x), то это означает, что для любого e > 0 все кривые у = fn (x) с достаточно большим номером будут расположены внутри полосы ширины 2e, ограниченной кривыми у = f (x) ± e для любого х из этого отрезка (см. рис.).
Равномерно сходящиеся последовательности функций обладают важными свойствами; например, предельная функция равномерно сходящейся последовательности непрерывных функций также непрерывна (приведенный выше пример показывает, что предельная функция последовательности непрерывных функций, которая не является равномерно сходящейся, может быть разрывной). Важную роль в математическом анализе играет теорема Вейерштрасса: каждая непрерывная на отрезке функция может быть представлена как предел равномерно сходящейся последовательности многочленов (или тригонометрических полиномов). См. также Приближение и интерполирование функций.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.12.2024 03:33:52
|
|
|
|
|
|
|
|
|
|
|
