|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Пуассона уравнение | Пуассона уравнение (далее П) уравнение с частными производными вида Du = f, где D —оператор Лапласа:
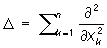
При n = 3 этому уравнению удовлетворяет потенциал u (х, у, z) объемных масс, распределенных с плотностью f (x, у, z)/4p (в областях, где f = 0 потенциал u удовлетворяет уравнению Лапласа), а также потенциал объемно распределенных электрических зарядов. При этом плотность распределения f должна удовлетворять известным требованиям гладкости (например, условию непрерывности частных производных). Если функция f отлична от нуля лишь в конечной области G, ограничена и имеет непрерывные частные производные первого порядка, то при n = 2 частное решение П имеет вид:
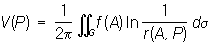
а при n = 3:
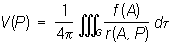
где r (А, Р) — расстояние между переменной точкой интегрирования А и некоторой точкой Р. В более подробной записи
(х, у, z) =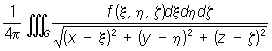 
Решение краевых задач для П сводится подстановкой 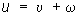 к решению краевых задач для уравнения Лапласа Dw = 0.
П впервые (1812) было изучено С. Д. Пуассоном.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.02.2025 05:13:27
|
|
|
|
|
|
|
|
|
|
|
