|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Прямоугольников формула | Прямоугольников формула (далее П)простейшая формула для приближенного вычисления определенного интеграла, имеющая вид
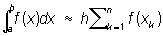
где h = (b — a)/n, xk = x + (k — 1) h и a £ x £ a + h. Наиболее точной из всех Прямоугольников формула является формула средних ординат, в которой x = а + h/2; если ÷f " (x)÷ < М на отрезке (а, b), то для этой формулы
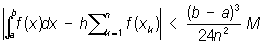
Остальные Прямоугольников формула в общем случае менее точны; поэтому, например, вместо формул, в которых x = а и x = а + h, предпочитают пользоваться их средним арифметическим (см. Трапеций формула), т.к. погрешность при этом будет не больше (b — a)3M/12n2. Если обе части Прямоугольников формула для x = а + h/2, x = а и x = а + h умножить соответственно на коэффициенты 2/3, 1/6, и 1/6, а затем сложить, то получится более точная формула приближенного интегрирования (см. Симпсона формула), погрешность которой не больше (b — a)5/2880n 4, где — максимум úf (x)ú на отрезке (а, b).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
