
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Производящая функция | Производящая функция (далее П)последовательности f0, f1..., fn... функция
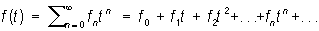
(в предположении, что этот степенной ряд сходится хотя бы для одного значения t ¹ 0). Производящая функция называют также генератрисой. Последовательность f0, f1..., fn... может быть как числовая, так и функциональная; в последнем случае Производящая функция зависит не только от t, но и от аргументов функций fn. Например, если fn = aqn где а и q - постоянные, то Производящая функция
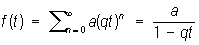
если fn - Фибоначчи числа; f0 = 0, f1 = 1, fn+2 = fn+1 + fn, то Производящая функция
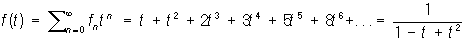
если fn = Т n (х) - Чебышева многочлены: T0 (х) = 1, Tn (х) = cos (n arc cos x), то Производящая функция
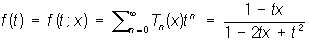
и т.д. Знание Производящая функция последовательности часто облегчает изучение свойств последней. Производящая функция применяются в теории вероятностей, в теории функций и в алгебре (в теории инвариантов). Впервые метод Производящая функция был применен П. Лапласом для решения некоторых проблем теории вероятностей.
Лит.: Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1-2, М., 1967; Натансон И. П., Конструктивная теория функций, М. - Л., 1949.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 17:03:53
|

|

|
 |
|

|
 |
 |
 |
|