
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Производная | Производная (далее П) основное понятие дифференциального исчисления, характеризующее скорость изменения функции; П есть функция, определяемая для каждого х как предел отношения: 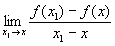 , если он существует. Функцию, имеющую П, называют дифференцируемой. , если он существует. Функцию, имеющую П, называют дифференцируемой.
Всякая дифференцируемая функция непрерывна; обратное утверждение неверно: существуют даже непрерывные функции, не имеющие П ни в одной точке (см. Непрерывная функция). Для функций действительного переменного сама П может быть недифференцируемой и даже разрывной. В комплексной же области существование первой П влечет существование П всех порядков. О П функций многих переменных (частная П), а также о правилах нахождения П и различных приложениях см. в ст. Дифференциальное исчисление.
В теории функций действительного переменного изучаются, в частности, функциональные свойства П и различные обобщения понятия "П". Так, например, всюду существующая П относится к функциям первого класса по Бэра классификации; П (даже если она разрывна) принимает все промежуточные значения между наименьшим и наибольшим. Из различных обобщений понятия "П" наиболее существенны следующие.
Производные числа. Верхним правым производным числом Dd называют верхний предел отношения 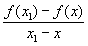 при при 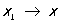 , где x1 > х. Аналогично определяют нижнее правое ld, верхнее Ds и нижнее ls левые производные числа. Если Dd = ld (D = ls), то f (x) имеет в точке х одностороннюю правую (левую) П Обыкновенная П существует, если все четыре производных числа конечны и совпадают. Производные числа были введены итал. математиком У. Дини (1878). Как показал Н. Н. Лузин (1915), если все четыре производных числа конечны на некотором множестве, то функция имеет обычную П всюду на этом множестве, кроме точек множества меры нуль (см. Мера множества). , где x1 > х. Аналогично определяют нижнее правое ld, верхнее Ds и нижнее ls левые производные числа. Если Dd = ld (D = ls), то f (x) имеет в точке х одностороннюю правую (левую) П Обыкновенная П существует, если все четыре производных числа конечны и совпадают. Производные числа были введены итал. математиком У. Дини (1878). Как показал Н. Н. Лузин (1915), если все четыре производных числа конечны на некотором множестве, то функция имеет обычную П всюду на этом множестве, кроме точек множества меры нуль (см. Мера множества).
Асимптотическая (или аппроксимативная) производная была введена А. Я. Хинчиным (1916). Асимптотической П называется предел отношения 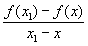 , когда x1 ® x пробегая точки множества, для которого х является плотности точкой. , когда x1 ® x пробегая точки множества, для которого х является плотности точкой.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:59:35
|

|

|
 |
|

|
 |
 |
 |
|