|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Проективное пространство | Проективное пространство (далее П), в первоначальном смысле — евклидово пространство, дополненное бесконечно удаленными точками, прямыми и плоскостью, называемыми также несобственными элементами (см. Бесконечно удаленные элементы). При этом каждая прямая дополняется одной несобственной точкой, каждая плоскость — одной несобственной прямой, все пространство — одной несобственной плоскостью; параллельные прямые дополняются общей несобственной точкой, непараллельные — разными; параллельные плоскости дополняются общей несобственной прямой, непараллельные — разными; несобственные точки, дополняющие всевозможные прямые данной плоскости, принадлежат несобственной прямой, дополняющей ту же плоскость; все несобственные точки и прямые принадлежат несобственной плоскости.
П можно определить аналитически как совокупность классов пропорциональных четверок действительных чисел, не равных одновременно нулю. При этом классы интерпретируются либо как плоскости П, а числа называются однородными координатами плоскостей. Отношение инцидентности точки (x1: x2: x3: x4) и плоскости (u1: u2: u3: u4) выражается равенством: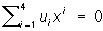 . Аналогичнымобразом вводится понятие n-мерного П, играющего важную роль в алгебраической геометрии, причем координатами его могут быть элементы некоторого тела k. В более общем смысле П — совокупность трех множеств элементов, называется соответственно точками, прямыми и плоскостями, для которых определены отношения принадлежности и порядка так, что соблюдаются требования аксиом проективной геометрии. А. Н. Колмогоров и Л. С. Понтрягин показали, что если П над телом k есть связное компактное топологическое пространство, в котором прямая непрерывно зависит от двух принадлежащих ей точек, и выполняются аксиомы инцидентности, то k есть либо поле действительных чисел, либо поле комплексных чисел, либо тело кватернионов.
Лит. см. при ст. Проективная геометрия.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 23.02.2025 10:06:18
|
|
|
|
|
|
|
|
|
|
|
