
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Почти периодическая функция | Почти периодическая функция (далее П), функция, значения которой при добавлении к аргументу надлежащим образом выбранных постоянных чисел (почти периодов) приближенно повторяются. Более точно: непрерывная функция f (x), определенная для всех действительных значений х, называется почти периодической, если для каждого e > 0 можно указать такое l = l (e), что в каждом интервале оси х длины l найдется хотя бы одно число t = t(e), для которого при любом х выполняется неравенство |f (x + t) — f (x)| < e. Числа t называются почти периодами функции f (x). Периодическая функции суть частные случаи П; простейшие примеры П, не являющихся периодическими, получаются в результате сложения периодических функций с несоизмеримыми периодами, например cosx + cos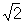 x. x.
Некоторые наиболее важные свойства П:
1) П ограничена и равномерно непрерывна на всей оси х.
2) Сумма и произведение конечного числа П есть также П
3) Предел равномерно сходящейся последовательности П есть также П
4) Для каждой П существует среднее значение (на всей оси х):
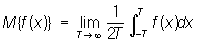 . .
5) Каждой П можно сопоставить ряд Фурье:
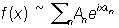 , ,
причем l1, l2, …, ln, …, может быть любой последовательностью отличных друг от друга действительных чисел и
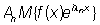 . .
6) Равенство Парсеваля: для каждой П справедливо равенство:
M {|f (x)|2} = 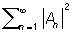 . .
7) Теорема единственности: если f (x) есть непрерывная П и если для всех действительных l
М {f (х) е-ilx} = 0,
то f (x) º 0. Иначе говоря, ряд Фурье однозначно определяет П
8) Теорема аппроксимации: для каждого e > 0 можно указать такой конечный тригонометрический полином
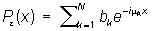
(mk — действительные числа), что для всех значений х выполняется неравенство: |f (x) — e(x)| < e; обратно, каждая функция f (x) с этим свойством является П
Первое построение непрерывных П было дано датским математиком Х. Бором (1923). Еще ранее (1893) частный случай П — т. н. квазипериодические функции — изучил латвийский математик П. Боль. Новое построение теории П дал Н. Н. Боголюбов (1930). Обобщение теории П на разрывные функции впервые дано В. В. Степановым (1925), а потом Г. Вейлем и А. Безиковичем. Обобщение другого рода было дано советским математиком Б. М. Левитаном (1938).
Лит.: Бор Г., Почти периодические функции, пер. с нем., М. — Л., 1934; Левитан Б. М., Почти-периодические функции, М., 1953.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 16.02.2026 05:34:18
|

|

|
 |
|

|
 |
 |
 |
|