
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Потенциалы электромагнитного поля | Потенциалы электромагнитного поля (далее П), величины, характеризующие электромагнитное поле. В электростатике векторное электрическое поле можно характеризовать одной скалярной функцией - потенциалом электростатическим. В общем случае для описания произвольного электромагнитного поля вместо двух векторов - магнитной индукции В и напряженности электрического поля Е можно ввести две др. величины: векторный потенциал А (х, у, z, t) и скалярный потенциал j(x, у, z, t) (где х, у, z - координаты, t - время), при этом В и Е однозначно выражаются через А и j
В = rot А,
E = -gradj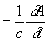 , (1) , (1)
где с - скорость света в вакууме.
Уравнения для потенциалов поля имеют более простую форму, чем исходные Максвелла уравнения, и поэтому введение П упрощает задачу нахождения переменных электромагнитных полей. Существенное упрощение уравнений для П возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо А и j выбрать новые потенциалы
А" = А + gradc,
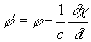 , (2) , (2)
где c - произвольная функция координат и времени, то векторы В и Е, определяемые уравнениями (1), не изменятся. Инвариантность электромагнитного поля по отношению к преобразованиям потенциалов (2) носит название или градиентной инвариантности. инвариантность позволяет наложить на П дополнительное условие. Обычно таким дополнительным условием является условие Лоренца:
divA + 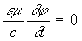 , (3) , (3)
где e и m- диэлектрическая и проницаемости среды. При использовании условия (3) уравнения для П в однородной среде (e = const, m = const), получаемые из уравнений Максвелла, приобретают одинаковую форму:
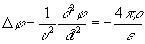 , (4) , (4)
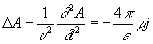 ; ;
здесь D-Лапласа оператор, r и j - плотности заряда и тока, a u = 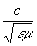 - скорость распространения электромагнитного поля в среде. Если r = 0 и j = 0, то П удовлетворяют волновым уравнениям. - скорость распространения электромагнитного поля в среде. Если r = 0 и j = 0, то П удовлетворяют волновым уравнениям.
Уравнения (4) позволяют определить потенциалы А и j по известному распределению зарядов и токов, а следовательно, с помощью формул (1) - характеристики электромагнитного поля В и Е. Частные решения уравнений (4), удовлетворяющие причинности принципу, называют запаздывающими потенциалами. Запаздывающие потенциалы в точке с координатами х, у, z в момент времени t определяются плотностями заряда и тока в точке с координатами х`, у`, z" в предшествующий момент времени t = t - R/u, где
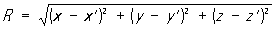
- расстояние от источника поля до точки наблюдения.
Если заряды и токи распределены в конечной области пространства G, то запаздывающие потенциалы определяются суммированием (интегрированием) элементарных потенциалов от зарядов и токов, сосредоточенных в бесконечно малых объемах dx"dy"dz`, с учетом времени запаздывания:
j (х, у, z, t) = 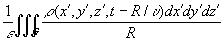 , ,
A (х, у, z, t) = 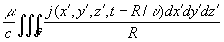 , ,
Через П выражается функция Гамильтона Н заряженной частицы, движущейся в электромагнитном поле:
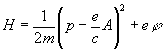 , (6) , (6)
где p - импульс частицы, e и m - ее заряд и масса. Соответственно через П выражается оператор Гамильтона (гамильтониан) в квантовой механике.
Лит. см. при ст. Максвелла уравнения.
Г. Я. Мякишев. |
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 17:00:57
|

|

|
 |
|

|
 |
 |
 |
|