
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Последовательный анализ | Последовательный анализ (далее П) в математической статистике, способ статистической проверки гипотез, при котором необходимое число наблюдений не фиксируется заранее, а определяется в процессе самой проверки. Во многих случаях для получения столь же обоснованных выводов применение надлежащим образом подобранного способа П позволяет ограничиться значительно меньшим числом наблюдений (в среднем, т.к. число наблюдений при П есть величина случайная), чем при способах, в которых число наблюдений фиксировано заранее.
Пусть, например, задача состоит в выборе между гипотезами 1 и 2 по результатам независимых наблюдений. Гипотеза 1 заключается в том, что случайная величина Х имеет распределение вероятностей с плотностью f1(x), a 2 — в том, что Х имеет плотность f2(x). Для решения этой задачи поступают следующим образом. Выбирают два числа А и В (0 < A < ). После первого наблюдения вычисляют отношение l1 = f2(x1)/f1(x1), где x1 — результат первого наблюдения. Если l1 < A, принимают гипотезу 1; если l1 > , принимают 2, если A £ l1 £ , производят второе наблюдение и так же исследуют величину l2 = f2(x1) f2(x2)/f1(x1) f1(x2), где x2 — результат второго наблюдения, и т.д. С вероятностью, равной единице, процесс оканчивается либо выбором 1, либо выбором 2. Величины А и В определяются из условия, чтобы вероятности ошибок первого и второго рода (т. е. вероятность отвергнуть гипотезу 1, когда она верна, и вероятность принять 1, когда верна 2) имели заданные значения a1 и a2. Для практических целей вместо величины ln удобнее рассматривать их логарифмы. Пусть, например, гипотеза 1 состоит в том, что Х имеет нормальное распределение
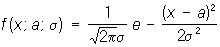
с a = 0, s = 1, гипотеза 2 — в том, что X имеет нормальное распределение с a = 0,6, s = 1, и пусть a1 = 0,01, a2 = 0,03. Соответствующие подсчеты показывают, что в этом случае
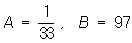
и logln = 0.6 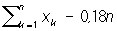
Поэтому неравенства 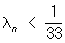 и и 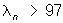 равносильны неравенствам равносильны неравенствам
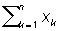 < 0.3n - 5.83 < 0.3n - 5.83
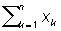 > 0.3n + 7.62 > 0.3n + 7.62
соответственно. Процесс П допускает при этом простое графическое изображение (см. рис.). На плоскости (хОу) наносятся две прямые y = 0.3x - 5.83 и y = 0.3x + 7.62 и ломаная линия с вершинами в точках (n, 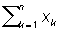 ), n = 1, 2,.... Если ломаная впервые выходит из полосы, ограниченной этими прямыми, через верхнюю границу, то принимается 2, если через нижнюю, — 1. В приведенном примере для различения 1 и 2 методом П требуется в среднем не более 25 наблюдений. В то же время для указанного различения гипотез 1 и 2 по выборкам фиксированного объема потребовалось бы более 49 наблюдений. ), n = 1, 2,.... Если ломаная впервые выходит из полосы, ограниченной этими прямыми, через верхнюю границу, то принимается 2, если через нижнюю, — 1. В приведенном примере для различения 1 и 2 методом П требуется в среднем не более 25 наблюдений. В то же время для указанного различения гипотез 1 и 2 по выборкам фиксированного объема потребовалось бы более 49 наблюдений.
Лит.: Блекуэлл Д., Гиршик М. А., Теория игр и статистических решений, пер. с англ., М., 1958: Вальд А., П, пер. с англ., М., 1960; Ширяев А. Н., Статистический последовательный анализ, М., 1969.
Ю. В. Прохоров.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 16:57:42
|

|

|
 |
|

|
 |
 |
 |
|