
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Положительно-определенная форма | Положительно-определенная форма (далее П), выражение вида
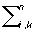 aikxixk, aikxixk,
где aik = aki, принимающее неотрицательные значения при любых действительных значениях x1, х2,..., xn и обращающееся в нуль лишь при x1 = х2 =... = xn = 0. Т. о., П.-о. ф. есть квадратичная форма специального типа. Любая П.-о. ф. приводится с помощью линейного преобразования к виду
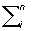 x2i x2i
Для того чтобы
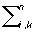 aikxixk aikxixk
была П.-о. ф. необходимо и достаточно, чтобы D1 > 0, …, Dn > 0, где
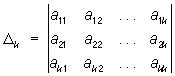
В любой аффинной системе координат расстояние точки от начала координат выражается П.-о. ф. от координат точки. Форма
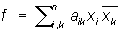 , ,
(где 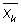 — число, комплексно сопряженное с xk, см. Комплексные числа) такая, что aik = — число, комплексно сопряженное с xk, см. Комплексные числа) такая, что aik = 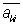 и f ³ 0 для всех значений x1, х2,..., xn и f = 0 лишь при x1 = х2 =...= xn = 0, называется эрмитовой П.- о. ф. и f ³ 0 для всех значений x1, х2,..., xn и f = 0 лишь при x1 = х2 =...= xn = 0, называется эрмитовой П.- о. ф.
С понятием П.-о. ф. связаны также понятия: 1) положительно-определенной матрицы ||aik|| — такой матрицы, что
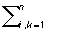 aikxixk aikxixk
есть эрмитова П.-о. ф.;
2) положительно-определенного ядра — такой функции К (х, у) = 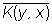 , что , что
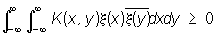
для любой функции x(х) с интегрируемым квадратом; 3) положительно-определенной функции — такой функции f (x), что ядро К (х, у) = f (x - y) является положительно-определенным. Класс непрерывных положительно-определенных функций f (x) c f (0) = 1 совпадает с классом характеристических функций законов распределения случайных величин.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 23:40:35
|

|

|
 |
|

|
 |
 |
 |
|