
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Полное пространство | Полное пространство (далее П) метрическое пространство, в котором выполнен признак сходимости Коши. Последовательность точек x1, х,..., xn,... на прямой, в плоскости или пространстве называемом фундаментальной, если при достаточно больших номерах n и m расстояние между точками xn и xm становится сколь угодно малым. Для того чтобы последовательность точек имела предел, необходимо и достаточно, чтобы она была фундаментальной (признак Коши). Для многих совокупностей математических объектов (функций, операторов и т.д.) можно ввести понятие расстояния, обладающее свойствами, аналогичными свойствам обычного расстояния. Тогда говорят, что эта совокупность является метрическим пространством. В метрическом пространстве можно обычным образом определить понятие предела последовательности точек. Если при этом имеет место признак Коши, то пространство называется полным. Примерами П служат евклидовы и многие другие линейные пространства, в частности пространство непрерывных функций на отрезке (a, b) с расстоянием
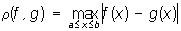
и гильбертово пространство. Замкнутое подмножество П является П Если метрическое пространство неполно, то его можно пополнить до П, аналогично тому, как пополняется множество рациональных чисел иррациональными до совокупности всех действительных чисел. Понятие полноты обобщается и на те неметрические топологического пространства, в которых можно сравнивать окрестности различных точек (например, на топологические группы, кольца и т.д.).
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 23:32:36
|

|

|
 |
|

|
 |
 |
 |
|