|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Полная система функций | Полная система функций (далее П), такая система функций Ф = {j(x:)}, определенных на отрезке (a, b), что не существует функции f (x), для которой, 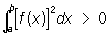 и которая была бы ортогональна ко всем функциям j(х) из Ф, т. е. для которой
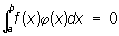
при любой функции j(х) из Ф (интегралы понимаются в смысле Лебега, см. Интеграл). Система функций может быть полной на одном отрезке и не быть полной на другом. Например, 1, sinx, cos х,..., sinnx, cosnx,... образуют П на отрезке (0, 2p), но не образуют П на отрезке (—2p, 2p); последнее вытекает из того, что
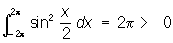
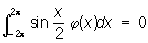
для любой функции j(x) рассматриваемой системы. Для того чтобы система функций с интегрируемым квадратом была П, необходимо и достаточно, чтобы любую функцию с интегрируемым квадратом на отрезке (а, b) можно было с любой степенью точности приблизить в среднем линейными комбинациями функций из этой системы. См. Ортогональная система функций.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 31.10.2025 11:06:54
|
|
|
|
|
|
|
|
|
|
|
