|
|
Большая Советская Энциклопедия (цитаты)
|
|
|
|
|
Подъемная сила | Подъемная сила (далее П), составляющая полной силы давления жидкой или газообразной среды на движущееся в ней тело, направленная перпендикулярно к скорости тела (к скорости центра тяжести тела, если оно движется непоступательно). Возникает П вследствие несимметрии обтекания тела средой. Например, при обтекании крыла самолета (рис. 1) частицы среды, обтекающие нижнюю поверхность, проходят за тот же промежуток времени меньший путь, чем частицы, обтекающие верхнюю, более выпуклую поверхность и, следовательно, имеют меньшую скорость. Но, согласно Бернулли уравнению, там, где скорость частиц меньше, давление среды больше и наоборот. В результате давление среды на нижнюю поверхность крыла будет больше, чем на верхнюю, что и приводит к появлению П
Несимметричное обтекание крыла можно представить как результат наложения на симметричное течение циркуляционного потока вокруг контура крыла, направленного на более выпуклой части поверхности в сторону течения, что приводит к увеличению скорости, а на менее выпуклой - против течения, что приводит к ее уменьшению. Тогда П будет зависеть от величины циркуляции скорости Г и, согласно Жуковского теореме, для участка крыла длиной L, обтекаемого плоскопараллельным потоком идеальной несжимаемой жидкости, = ruГL, где r - плотность среды, u - скорость набегающего потока.
Поскольку Г имеет размерность (u×l), то П можно выразить равенством = cyru2/2 обычно применяемым, в аэродинамике где - величина характерной для тела площади (например, площадь крыла в плане), су - безразмерный коэффициент П, зависящий от формы тела, его ориентации в среде и чисел Рейнольдса и Маха М. Значение су определяют теоретическим расчетом или экспериментально. Так, согласно теории Жуковского, для крыла в плоско-параллельном потоке су = 2m (a - a0), где a - угол атаки (угол между направлением скорости набегающего потока и хордой крыла), a0 - угол нулевой П, m - коэффициент, зависящий только от формы профиля крыла, например, для тонкой изогнутой пластины m = p. В случае крыла конечного размаха / коэффициент m = p/(1 - 2/l), где l = l2/ - удлинение крыла.
В реальной жидкости в результате влияния вязкости величина m меньше теоретической, причем эта разница возрастает по мере увеличения относительной толщины профиля; значение угла a0 также меньше теоретического. Кроме того, с увеличением угла a зависимость су от a (рис. 2), перестает быть линейной и величина dcy/da монотонно убывает, становясь равной нулю при угле атаки aкр, которому соответствует максимальная величина коэффициента П - cymax. Дальнейшее увеличение а ведет к падению су вследствие отрыва пограничного слоя от верхней поверхности крыла. Величина cymax имеет существенное значение, т.к. чем она больше, тем меньше скорость взлета и посадки самолета.
При больших, но докритических скоростях, т. е. таких, для которых М < Мкр (Mkp - значение числа М набегающего потока, при котором вблизи поверхности профиля местные значения числа М = 1), становится существенной сжимаемость газа. Для слабо изогнутых и тонких профилей при малых углах атаки сжимаемость можно приближенно учесть, положив
 ,  .
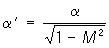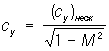При сверхзвуковых скоростях характер обтекания существенно меняется. Так, при обтекании плоской пластины у передней кромки на верхней поверхности образуются волны разрежения, а на нижней - ударная волна (рис. 3). В результате давление рн на нижней поверхности пластины становится больше, чем на верхней (рв); возникает суммарная сила, нормальная к поверхности пластины, составляющая которой, перпендикулярная к скорости набегающего потока, и есть П Для малых М > 1 и малых a П пластины может быть вычислена по формуле 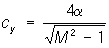 . Эта формула справедлива и для тонких профилей произвольной формы с острой передней кромкой.
Лит.: Жуковский Н.Е., О присоединенных вихрях, Избр. соч., т. 2, М. - Л., 1948; Лойцянский Л. Г., Механика жидкости и газа, 2 изд., М., 1957; Голубев В. В., Лекции по теории крыла, М. - Л., 1949; Абрамович Г. Н., Прикладная газовая динамика, 2 изд., М., 1953; Ферри А., Аэродинамика сверхзвуковых течений, пер. с англ., М., 1953.
М. Я. Юделович.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|
|
 |
 |
 |
|
|
|
Новости 22.12.2024 21:32:52
|
|
|
|
|
|
|
|
|
|
|
