
|

|
Большая Советская Энциклопедия (цитаты)
|

|

|
 |
Подстановка | Подстановка (далее П) элементов данного множества (математическая), замена каждого из его элементов а каким-либо другим элементом j(а) из того же множества; при этом должны получаться все элементы исходного множества и каждый только один раз. Таким образом, понятие П по существу совпадает с понятием взаимно однозначного отображения множества на себя (см. Взаимно однозначное соответствие), однако оно применяется большей частью к конечным множествам. Только этот случай и рассматривается ниже. Для П принята запись
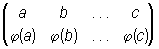 , ,
здесь под каждым из элементов данного множества написан соответствующий ему элемент. Так как свойства П не зависят от природы элементов а, b,..., с, то большей частью (во всяком случае — в учебных целях) используют целые числа 1, 2,..., n, при этом в верхней строке они преимущественно записываются в своем естественном порядке; П принимает вид
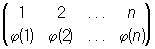
или проще
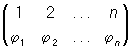 , ,
где j1, j2,..., jn — те же числа 1, 2,..., n, но записанные, возможно, в каком-либо ином порядке. Т. о., вторая строка П образует перестановку j1, j2,..., jn из чисел 1, 2,..., n. Различных П из n элементов существует столько же, сколько и перестановок, т.е. n! = 1×2×3×...×n. П
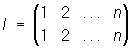 , ,
оставляющая на месте все элементы, называется единичной, или тождественной. Для каждой подстановки А существует обратная, т. е. такая, которая переводит ji в i; она обозначается через А-1. Например,
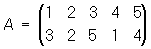 ; ;
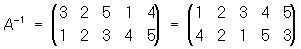 . .
Результат последовательного применения двух подстановок А и В снова будет некоторой подстановкой С: если А переводит i в ji, а В переводит ji в yi, то С переводит i в yi. П С называется произведением подстановок А и В, что записывается так: С = АВ. Например, если
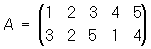 ; ; 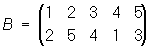 , ,
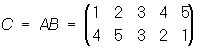 . .
При умножении П не выполняется закон коммутативности, т. е., вообще говоря, АВ ¹ ВА; так, в том же примере
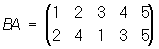 . .
Легко видеть, что IA = AI = А, АА-1= А-1А = , А (ВС) = (АВ) С (ассоциативный закон). Т. о., все П из n элементов образуют группу, называемую симметрической группой степени n.
П, переставляющая местами только 2 элемента i и j, называют транспозицией и обозначается так: (i, j), например
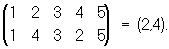
Любую П можно разложить в произведение транспозиций. Число множителей при разложении разными способами данной П в произведение транспозиций всегда будет либо четным, либо нечетным. В соответствии с этим и П называют либо четной, либо нечетной; например, А = (1, 3)(5, 4)(5, 1) — нечетная П Четность П можно определить также по числу инверсий, т. е. по числу нарушений порядка в нижней строке П, если числа верхней строки расположены в их естественном порядке: четность П совпадает с четностью числа инверсий; например, в нижней строке подстановки А имеется 5 инверсий, т. е. случаев, когда большее число стоит раньше меньшего: (3, 2), (3, 1),(2, 1), (5, 1) и (5, 4). Существует n!/2 четных и n!/2 нечетных П из n элементов.
П, циклически переставляющая данную группу элементов, а остальные элементы оставляющая на месте, называется циклом. Число переставляемых элементов называют длиной цикла. Например, подстановка А есть цикл длины 4: она переводит 1 в 3, 3 в 5, 5 в 4, 4 в1; коротко это записывается так: А = (1, 3, 5, 4). Транспозиция есть цикл длины 2. Любую П можно разложить в произведение независимых (т. е. не имеющих общих элементов) циклов. Например,
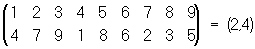
Термин "П" в интегральном исчислении означает замену переменной в подынтегральной функции.
Лит.: Курош А. Г., Курс высшей алгебры, 10 изд., М. — Л., 1971.
|
Для поиска, наберите искомое слово (или его часть) в поле поиска
|

|
 |
 |
 |

|

|
Новости 23.02.2026 18:15:20
|

|

|
 |
|

|
 |
 |
 |
|